多片检校方程 相对定向完成标志  相对定向解答的两种方式 图解连续像片和单独像对

单片检校主要目的是精确测量相机的内方位元素和检校相机镜头畸变。由于只使用一幅影像进行参数的解算，使用了较少的几何约束条件和观测值，最容易产生内方位元素x0 y0 与外方位元素Xs Ys的不定解或强相关，使检校结果稳定性和可靠性受到影响。多片后方交会则可以更精确的解算这些参数，尤其是主点位置的精度问题。多片空间后方交会与单片空间后方交会的根本区别是：在不同的位置拍摄多张照片，由于各像片在同一主距条件下拍摄，因而解算所得的各相片的外方位元素不同，解算的内方位元素和畸变参数被认为相同。

这样，就可以用下式方程表达多片交会：

$$\begin{bmatrix}A_{I}&0&.&.&.&0&B_{I}&C_{I}\\0&A_{II}&.&.&.&0&B_{II}&C_{II}\\\ .&.&.&.&.&.&.&.\\0&.&.&.&.&A_{n}&B_{n}&C_{n}\end{bmatrix}_{2n\times (6n+7)}\begin{bmatrix}X_{out_{I}}\\X_{out_{II}}\\\ .\\\ .\\\ .\\X_{out_{n}}\\X_{in}\\X_{res}\end{bmatrix}_{(6n+7)\times1}-\begin{bmatrix}xy_{res 1}\\xy_{res 2}\\\ .\\\ .\\\ .\\xy_{res n}\end{bmatrix}_{2\times1}=0$$

这一点与图像配准极其相似，用一副影像作为参考影像去配准多幅图像的结果显然没有用周边多幅图像组为参考标准的结果令人信服。由于每张相片的外方位元素不同（一般都是围绕检校场左中右进行拍摄），所以良好的消除了外方位元素和内方位元素的强相关性。

针对多片，提出了相对定向和绝对定向的概念，绝对定向即利用共线方程检校计算出的外方位元素绝对值，这是以物方坐标系的原点作为参考值；而相对定向则是以被检校出的某一张像片为参考，计算出其余像片在其坐标系的坐标值，即相对关系。相对关系的求取的精度对图像拼接有至关重要的影像。

相对定向完成的标志：同名光线对对相交。所有点在其承影面上的上下视差为零。即通过矩阵变换改变投影器的相对位置，使光线相交。   

相对定向有两种方式：①根据单片分别解算出的不同像片（可以使同相机可以不同）物方坐标系下的外方位元素绝对值，计算相对定向的五个元素，By,Bz,φ2，ω2，k2;或多片解算的某一相机的物方绝对值（必须统一相机，保证内方位元素相同），同样计算相对定向元素。可以作为航拍的连续拍摄的相对方位的确定，也可以作为立体固定的某些相机之间的相对方位的确定②直接根据同名点的像点坐标（6组以上），计算相对定向的旋转矩阵[R|t]，不需要地面控制点！。

图解①方式的连续像对和单独像对

上面提到的连续像对，如下图所示，By Bz决定了摄影基线（即摄影中心移动的向量），φ2，ω2，k2决定了右片光束对于左光束的旋转。固定一个光束，旋转和移动第二个，便可以确定两个光束之间的相对方位，第三张相片可以和第二张相片确定相对方位，一次类推，所形成的相对方位元素称为连续像对系统。

而单独相对，即可以取左片摄影中心XZ平面为主核面，摄影基线为X轴的右手空间直角坐标系。由φ1，ω1，k1,φ2，ω2，k2组成。

 

相对定向共面条件

在相对定向中，答解相对元素的重要依据就是共面条件，当光线相交时，易知B（摄影基线，即S1S2）,S1a1,S2a2共面。如图可以看到，解求相对定向元素就是解求两个摄影中心的像方辅助坐标系的转换。共面条件方程形式为：

$$\overrightarrow{S_{1}S_{2}}\cdot (\overrightarrow{S_{1}a_{1}}\times \overrightarrow{S_{2}a_{2}})=0$$

共面条件方程无需地面控制点，一个同名点列一个方程。必须有5个以上定向点。

如图，设像点a1、a2在大地坐标系坐标分别为(X1,Y1,Z1)、(X2,Y2,Z2).摄站S1、S2在大地坐标系坐标分别为

$$(X_{S1},Y_{S1},Z_{S1}),(X_{S2},Y_{S2},Z_{S2})$$ ,则上式在即可表示为向量形式的行列式。

$$\begin{vmatrix}X_{S2}-X_{S1}&Y_{S2}-Y_{S1}&Z_{S2}-Z_{S1}\\X_{1}-X_{S1}&Y_{1}-Y_{S1}&Z_{1}-Z_{S1}\\X_{2}-X_{S2}&Y_{2}-Y_{S2}&Z_{2}-Z_{S2}\end{vmatrix}$$

又令(X,Y,Z)、(Bx,By,Bz)为a1,S2在S1的像辅系S1-XYZ中的坐标，(X’,Y’,Z’)为a2在S2像辅系S2-XYZ中的坐标。由三点共面的方程，

$$\begin{vmatrix}B_{X}&B_{Y}&B_{Z}\\X&Y&Z\\X’&Y’&Z’\end{vmatrix}=0$$ 上式可改写为：

$$\begin{bmatrix}B_{X}&B_{Y}&B_{Z}\end{bmatrix}\begin{bmatrix}0&-Z&Y\\Z&0&-X\\\ -Y&X&0\end{bmatrix}\begin{bmatrix}X’\\Y’\\Z’\end{bmatrix}=0$$

光线是否成对相交与摄影测量坐标系的选择无关，但可以选择适当的像辅系，改变共面条件便于实际应用。

（1）选择左侧像空系——连续像对系统。此时R1=E，即左系的旋转矩阵为0，像平面的z坐标均为-f；或为右片的旋转矩阵。则，公式未改变。

$$\begin{vmatrix}B_{X}&B_{Y}&B_{Z}\\X&Y&Z\\X’&Y’&Z’\end{vmatrix}=0$$

（2）选择基线坐标系——单独像对系统。此时，

$$B_{Y}=B_{Z}=0$$ ，即需要求取两个像片对基线坐标系的旋转。

为毛要做畸变差矫正?

单片检校主要目的是精确测量相机的内方位元素和检校相机镜头畸变。而多片后方交会则可以更精确的解算这些参数，还可以同时在平差中解求各个物方测量点的精确估值，也可以利用这些大容量的信息进行基于空间位置的组合镜头多片拼接和航带拼接。本篇主要介绍多片后方交会的应用。

航摄中常用的三种用于加密控制点的方法有航带法、独立模型法、光束法。其中航带法精度较低，不能用于高精度的测量。独立模型法较前者精度略高，光束法则是精度最高同时计算量最大的模型，适用于高精度航摄。
但粗差同样对于精度的影响极大，自检较光束则是最广泛应用的做法。其基本思想是选用一个由若干个参数组成的系统误差模型，将这些附加参数作为未知数与区域网的其他参数一起解求，从而达到在平差过程中自动消除系统误差的目的。其缺点是①附加参数人为选择，选择不当会导致迭代结果不收敛恶化计算结果。②附加参数与区域网参数一起解求，会使计算量明显上升。

本片涉及前文中叙述到的三个角元素含义及外延，包含与角元素相关的旋转矩阵R并简明介绍几个常用坐标系。

内容提要：

几个概念（视场 像场 视场角） 

几个坐标系

共线方程的推导

 坐标旋转即共线方程的应用

坐标旋转

像片水平与倾斜像点坐标的关系

几个概念： 

视场：光线通过物镜后，焦面上照度不均匀的光亮圆为镜头的视场。

像场：摄影时，影像相当清晰的一部分视场内的光亮圆。

视场角（filed of view）：由镜头后节点向市场边缘射出的光线所张开的角，用2β表示。常角<75°，宽角75°~100°，特宽角>100°



数码相机的瞬时视场角IFOV与空间分辨率的关系： $$R_{g}=2\sqrt{2}IFOV$$

几个坐标系： 像素坐标系-2D-IAJ以像片左上角为坐标原点，下为y正，右为x正。坐标一般用(u,v)表示。

$$x=J\Delta -x_{0}$$ , $$y=-(I\Delta -y_{0})$$



这里，值得一提的是，坐标单位一般是像素。而一般以中心为基准的坐标系（像平面坐标系，一般用(x,y)表示的单位是毫米。这两个坐标系之间的转换公式形式可以写为:

$$!\left\{\begin{matrix}u=\frac{x}{d_{x}}+u_{0}=xs_{x+u_{0}}\\v=\frac{y}{d_{y}}+v_{0}=ys_{y}+v_{0}\end{matrix}\right. $$这里，dx dy分别代表每个像素在横轴x和纵轴y的物理尺寸，单位是mm per pixel。而sx和sy分别是二者的导数。或可以用矩阵的形式：$$ ! $$\begin{pmatrix}u\\v\\1\end{pmatrix}$$ = $$\begin{pmatrix}s_{x}&0&c_{x}\\0&s_{y}&c_{y}\\0&0&1\end{pmatrix}$$ $$\begin{pmatrix}x\\y\\1\end{pmatrix}$$ $$

像空间坐标系-3D-Sxyz表示像点在像方空间位置的空间直角坐标系。原点即投影中心，xy轴分别平行于像平面xy轴，z轴即主光轴的方向。在该坐标系中，所有像点的z坐标都是-f。几何含义就是，投影中心在投向焦平面的时候，与设计上认为的像点（像平面几何中心）相比，投偏了多少。像平面坐标+内方位元素就可以定位所有穿过像平面到达物放世界的光束的形状；该坐标系的方位就代表了像片的空间方位，像空间坐标系绕原点的旋转就代表了像片绕投影中心的旋转。下图中S为投影中心，O为投影中心，a为任意一个像点，其坐标为(x,y,-f)



物方空间坐标系-3D-O-XdYdZd测绘系统选择一定的原点，进行测绘测量的世界真实坐标，描述点的空间位置。摄影测量的成果最终要转到该坐标系中。

地面辅助坐标系-3D-O-XtYtZt 一般称地辅系，Z轴铅锤，X Y轴与物空系平行。在摄影测量中，原点都默认设为摄影中心S。因此该坐标系与物空系不需要进行旋转，只需要平移，即坐标轴加减运算。这是中间成果和数学运算常用的坐标系。下图是地辅系、像空系、像平面坐标系在一起的示意图。而共线方程就是依据这几个坐标系空间转换得到的。原理为三角形相似。



像素坐标系→像平面坐标系（内方位元素） 地面辅助坐标系→像平面坐标系（外方位元素）

共线方程的物理含义就是三点一线，两点一系（理想状况下，摄影瞬间像点、投影中心位于同一直线。）如图所示：

图中浅蓝色坐标系是地辅系（这里 地辅系通过投影中心 连接物空系和像空系），a点是像平面上的投影，A点是地面控制点，红色坐标系是物方空间坐标系，黄色坐标是像空系（像空系垂直与像平面），λ即投影比例尺，二维坐标各自成比例，形成了共线方程的最基本形式。也可以用向量的方式来解释。其中Xs  Ys  Zs是投影中心在物方空间的坐标，

$$X_{A}  Y_{A}  Z_{A}$$ 是真实世界某控制点的物方坐标。两者相减，即得到相对位置，即地辅系的坐标。该方程是建立在地辅系上的。

共线方程的推导

→点的坐标变换（一点两系）：目标是建立同一个点在空间坐标系与地面辅助坐标系中坐标值之间的对应关系。坐标点一般的转换关系为：

$$!\begin{pmatrix}X\\Y\\Z\end{pmatrix}=R\begin{pmatrix}x\\y\\z\end{pmatrix}$$

$$!\begin{pmatrix}x\\y\\z\end{pmatrix}=R^{T}\begin{pmatrix}X\\Y\\Z\end{pmatrix}$$

则R称为旋转矩阵。

点a、A位于两个坐标系，分别用两组坐标来表示。S-xyz示意像空系，S-XYZ示意地辅系。

点\坐标系	S-xyz	S-XYZ
a	x,y,-f	Xa，Ya，Za
A	xA,yA,zA	X,Y,Z

由于旋转矩阵相同，两个点可表示为：

$$!\begin{pmatrix}X\\Y\\Z\end{pmatrix}=R\begin{pmatrix}x_{A}\\y_{A}\\z_{A}\end{pmatrix}$$

$$!\begin{pmatrix}X_{a}\\Y_{a}\\Z_{a}\end{pmatrix}=R\begin{pmatrix}x\\y\-f\end{pmatrix}$$

则，

$$!\begin{pmatrix}x_{A}\\y_{A}\\z_{A}\end{pmatrix}=R^{T}\begin{pmatrix}X\\Y\\Z\end{pmatrix}$$

→点的共线关系（两点一系）：目标是建立像点和物方点的坐标关系。易知，两点一线时，可以用一个点的齐次方程表示另一个点。即：

$$!\left\{\begin{matrix}x_{A}=a_{1}X+b_{1}Y+c_{1}Z\\y_{A}=a_{2}X+b_{2}Y+c_{2}Z\\y_{A}=a_{3}X+b_{3}Y+c_{3}Z\end{matrix}\right.$$

上图中可建立的方程有，（该方程建立在像空系中）

$$!\frac{x_{A}}{x}=\frac{y_{A}}{y}=\frac{z_{A}}{-f}=\lambda \Rightarrow\left\{\begin{matrix}x=-f\frac{x_{A}}{z_{A}}\\y=-f\frac{y_{A}}{z_{A}}\end{matrix}\right.$$

联立坐标转换方程和像空系方程，化简即可得到传说中的共线条件方程。

用地面点坐标表示像点坐标的共线方程（地辅系形式）

$$!x=-f\frac{a_{1}(X_{T}-X_{S})+b_{1}(Y_{T}-Y_{S})+c_{1}(Z_{T}-Z_{S})}{a_{3}(X_{T}-X_{S})+b_{3}(Y_{T}-Y_{S})+c_{3}(Z_{T}-Z_{S})}$$

$$!y=-f\frac{a_{2}(X_{T}-X_{S})+b_{2}(Y_{T}-Y_{S})+c_{2}(Z_{T}-Z_{S})}{a_{3}(X_{T}-X_{S})+b_{3}(Y_{T}-Y_{S})+c_{3}(Z_{T}-Z_{S})}$$

或（物空系形式）

$$!x=-f\frac{a_{1}(X-X_{S})+b_{1}(Y-Y_{S})+c_{1}(Z-Z_{S})}{a_{3}(X-X_{S})+b_{3}(Y-Y_{S})+c_{3}(Z-Z_{S})}$$

$$!y=-f\frac{a_{2}(X-X_{S})+b_{2}(Y-Y_{S})+c_{2}(Z-Z_{S})}{a_{3}(X-X_{S})+b_{3}(Y-Y_{S})+c_{3}(Z-Z_{S})}$$

同理，利用蓝图中在地辅系的共线方程，可以建立用像点坐标表达地面坐标的方程（物空系形式）

$$!X=X_{s}+(Z-Z_{s})\frac{a_{1}x+a_{2}y-a_{3}f}{c_{1}x+c_{2}y-c_{3}f}$$

$$!Y=Y_{s}+(Z-Z_{s})\frac{b_{1}x+b_{2}y-b_{3}f}{c_{1}x+c_{2}y-c_{3}f}$$

上式也成为了前方交会解算的基本方程。

---

坐标旋转即共线方程的应用

①求像点坐标

• 已知Xs Ys Zs ai bi ci f(物方真值 旋转矩阵)
• 求x y（像平面坐标）

依赖方程：

$$!x=-f\frac{a_{1}(X-X_{S})+b_{1}(Y-Y_{S})+c_{1}(Z-Z_{S})}{a_{3}(X-X_{S})+b_{3}(Y-Y_{S})+c_{3}(Z-Z_{S})}$$

$$!y=-f\frac{a_{2}(X-X_{S})+b_{2}(Y-Y_{S})+c_{2}(Z-Z_{S})}{a_{3}(X-X_{S})+b_{3}(Y-Y_{S})+c_{3}(Z-Z_{S})}$$

②答解外方位元素(后方交会基本原理)

• 已知 $$x_{i}^{‘} y_{i}^{‘} X_{i} Y_{i} Z_{i} x_{0} y_{0} f$$ （像坐标观测值 物方观测值 内方位元素）
• 求Xs Ys Zs ai bi ci（外方位元素）

依赖方程：

$$!x^{‘}-x_{0}=-f\frac{a_{1}(X-X_{S})+b_{1}(Y-Y_{S})+c_{1}(Z-Z_{S})}{a_{3}(X-X_{S})+b_{3}(Y-Y_{S})+c_{3}(Z-Z_{S})}$$

$$!y^{‘}-y_{0}=-f\frac{a_{2}(X-X_{S})+b_{2}(Y-Y_{S})+c_{2}(Z-Z_{S})}{a_{3}(X-X_{S})+b_{3}(Y-Y_{S})+c_{3}(Z-Z_{S})}$$

③求地面点坐标

• 已知x，y，Xs，Ys，Zs，ai，bi，ci，f(外方位元素，像点坐标观测值，焦距)
• 求X，Y，Z（求未知物方点坐标,这里，大部分都知道DEM，即(X,Y)坐标下的Z高程的信息）

依赖方程(单片定位)：

$$!\frac{X-X_{S}}{Z-Z_{S}}=\frac{a_{1}x+a_{2}y-a_{3}f}{c_{1}x+c_{2}y-c_{3}f}$$

$$!\frac{Y-Y_{S}}{Z-Z_{S}}=\frac{b_{1}x+b_{2}y-b_{3}f}{c_{1}x+c_{2}y-c_{3}f}$$

依赖方程（立体像对定位）–4个方程解算3个未知数。(前方交会后方交会同时进行)

$$!\frac{X-X_{S}}{Z-Z_{S}}=\frac{a_{1}x+a_{2}y-a_{3}f}{c_{1}x+c_{2}y-c_{3}f}$$

$$!\frac{Y-Y_{S}}{Z-Z_{S}}=\frac{b_{1}x+b_{2}y-b_{3}f}{c_{1}x+c_{2}y-c_{3}f}$$

$$!\frac{X-X_{S}^{‘}}{Z-Z_{S}^{‘}}=\frac{a_{1}^{‘}x^{‘}+a_{2}^{‘}y^{‘}-a_{3}^{‘}f}{c_{1}^{‘}x^{‘}+c_{2}^{‘}y^{‘}-c_{3}^{‘}f}$$

$$!\frac{Y-Y_{S}^{‘}}{Z-Z_{S}^{‘}}=\frac{b_{1}^{‘}x^{‘}+b_{2}^{‘}y^{‘}-b_{3}^{‘}f}{c_{1}^{‘}x^{‘}+c_{2}^{‘}y^{‘}-c_{3}^{‘}f}$$

---

坐标旋转

从物方空间坐标系到像空间坐标系的转换其实就是一个平移（平移到地辅系）再旋转的过程，这就是常见的[R|t]。旋转真正的含义就是对3个坐标轴作二维角度上的旋转，3个旋转合成一个旋转矩阵R。坐标轴旋转θ角度，等同于目标点绕坐标原点反方向旋转同样的角度θ。选择的旋转3个坐标系的方式有很多，常用的就是以Y轴为主轴的φ，ω,k的系统。

航向倾角φ（pitching）：z轴在XZ坐标面内的投影（即过z轴所做的XZ面的垂面与XZ面的交线）与Z轴的夹角，叫做航向倾角。从Z轴算起，由Y轴的负方向逆时针为正。如图为正。

旁向倾角ω（roll）：z轴与XZ坐标面之间的夹角，即z轴与它在XZ面上投影之间的夹角，叫做旁向倾角。从z轴的投影算起，由X轴的正方向看逆时针为正。如图为正。

像片旋角k（yaw）：Y轴在xy坐标系面上的投影与y轴的夹角，叫做旋角。从投影算起，由z轴正方向看逆时针为正。如图k为正。

• 二维平面的坐标旋转

如图所示，旋转是可逆变化，两套坐标之间可以用矩阵和逆矩阵进行转换。

$$!\begin{bmatrix}x^{‘}\\y^{‘}\end{bmatrix}=A\begin{bmatrix}x\\y\end{bmatrix},\begin{bmatrix}x\\y\end{bmatrix}=A^{-1}\begin{bmatrix}x^{‘}\\y^{‘}\end{bmatrix}$$

$$!A=\begin{bmatrix}a_{1}&a_{2}\\b_{1}&b_{2}\end{bmatrix}=\begin{bmatrix}cos \widehat{x^{‘}x}&cos \widehat{x^{‘}y}\\cos\widehat{y^{‘}x}&cos \widehat{y^{‘}y}\end{bmatrix}=\begin{bmatrix}cos \kappa&sin \kappa\-sin \kappa&cos\kappa\end{bmatrix}$$

式中

a1是x’轴与x轴夹角的余弦；a1=cos k

b1是x’轴与y轴夹角的余弦：b1=cos(90°-k)=sin k

a2是y’轴与x轴夹角的余弦：a2=cos(90°+k)=-sin k

b2是y’轴与y轴夹角的余弦：b2=cos k

• 三维空间的坐标旋转

从像空间直角坐标系到像空间辅助坐标系之间的转换可以通过三次二维坐标转换完成。

$$!\begin{bmatrix}X\\Y\\Z\end{bmatrix}=R\begin{bmatrix}x\\y\-f\end{bmatrix}$$

$$!R=\begin{bmatrix}a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\c_{1}&c_{2}&c_{3}\end{bmatrix}=\begin{bmatrix}cos\widehat{Xx}&cos\widehat{Xy}&cos\widehat{Xz}\\cos\widehat{Yx}&cos\widehat{Yy}&cos\widehat{Yz}\\cos\widehat{Zx}&cos\widehat{Zy}&cos\widehat{Zz}\end{bmatrix}$$

①S-XYZ绕Y轴旋转φ到S-XφYφZφ，在XSZ平面内，以S点位圆心旋转XSZ至XφSZφ

$$!\begin{bmatrix}X\\Y\\Z\end{bmatrix}=R_{\varphi}\begin{bmatrix}X_{\varphi }\\Y_{\varphi }\\Z_{\varphi }\end{bmatrix}=\begin{bmatrix}cos\varphi&0&-sin\varphi\\0&1&0\\sin\varphi&0&cos\varphi\end{bmatrix}\begin{bmatrix}X_{\varphi }\\Y_{\varphi }\\Z_{\varphi }\end{bmatrix}$$

该次变换中，由于是绕Y轴旋转的，因此Y坐标值没有改变，相当于在二维XSZ平面做了旋转，下同。

②S-XφYφZφ绕Xφ旋转ω角到S-XφωYφωZφω，在YφSZφ平面内，以S点为圆心旋转YφSZφ到YφωSZφω。这次变化中，x轴坐标值没有改变。

$$!\begin{bmatrix}X_{\varphi}\\Y_{\varphi}\\Z_{\varphi}\end{bmatrix}=R_{\omega}\begin{bmatrix}X_{\varphi\omega}\\Y_{\varphi \omega}\\Z_{\varphi\omega}\end{bmatrix}=\begin{bmatrix}1&0&0\\0&cos \omega&-sin \omega\\0&sin \omega&cos \omega \end{bmatrix}\begin{bmatrix}X_{\varphi\omega}\\Y_{\varphi \omega}\\Z_{\varphi\omega}\end{bmatrix}$$

③S-XφωYφωZφω绕Zφω轴旋转k角度到S-xyz，在XφSYω平面内，以S点为圆心转到XφωSYφω至xSy。

$$!\begin{bmatrix}X_{\varphi\omega}\\Y_{\varphi\omega}\\Z_{\varphi\omega}\end{bmatrix}=R_{\kappa}\begin{bmatrix}x\\y\-f\end{bmatrix}=\begin{bmatrix}cos \kappa&-sin \kappa&0\\sin \kappa&cos \kappa&0\\0&0&1\end{bmatrix}\begin{bmatrix}x\\y\-f\end{bmatrix}$$

联立之前三个旋转矩阵即可得到三维下的旋转矩阵R

$$!\begin{bmatrix}X\\Y\\Z\end{bmatrix}=R_{\varphi}R_{\omega}R_{\kappa}\begin{bmatrix}x\\y\-f\end{bmatrix}=\begin{bmatrix}cos\varphi&0&-sin\varphi\\0&1&0\\sin\varphi&0&cos\varphi\end{bmatrix}\begin{bmatrix}1&0&0\\0&cos \omega&-sin \omega\\0&sin \omega&cos \omega \end{bmatrix}\begin{bmatrix}cos \kappa&-sin \kappa&0\\sin \kappa&cos \kappa&0\\0&0&1\end{bmatrix}\begin{bmatrix}x\\y\-f\end{bmatrix}=\begin{bmatrix}a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\c_{1}&c_{2}&c_{3} \end{bmatrix}\begin{bmatrix}x\\y\-f\end{bmatrix}=R\begin{bmatrix}x\\y\-f\end{bmatrix}$$

旋转矩阵R因此由外方位元素φ，ω，k确定。其中a1,a2,a3,b1,b2,b3,c1,c2,c3是9个方向的方向余弦。

$$!a_{1}=cos\varphi cos\kappa-sin\varphi sin\omega sin\kappa$$

$$!a_{2}=-cos\varphi sin\kappa -sin\varphi sin\omega cos\kappa$$

$$!a_{3}=-sin\varphi cos\omega$$

$$!b_{1}=cos\omega sin\kappa$$

$$!b_{2}=cos\omega cos\kappa$$

$$!b_{3}=-sin\omega$$

$$!c_{1}=sin\varphi cos\kappa+cos\varphi sin\omega sin\kappa$$

$$!c_{2}=-sin\varphi sin\kappa +cos\varphi sin\omega cos\kappa$$

$$!c_{3}=cos\varphi cos\omega$$

通过解算可知

$$!R\cdot R^{T}=\begin{bmatrix}a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\c_{1}&c_{2}&c_{3} \end{bmatrix}\cdot \begin{bmatrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\a_{3}&b_{3}&c_{3}\end{bmatrix}=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}$$

$$!R^{T}\cdot R =\begin{bmatrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\a_{3}&b_{3}&c_{3}\end{bmatrix}\cdot \begin{bmatrix}a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\c_{1}&c_{2}&c_{3} \end{bmatrix}=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}$$

很明显，意味着R与

$$R^{T}$$ 互为逆矩阵。这也验证了R矩阵是两个坐标系之间相互转换的矩阵。由 $$RR^{T}=I$$ 可得：

（1）同行（列）列的各元素自乘之和为1

（2）任意两行（列）的对应元素相乘之和为0（正交）

（3）旋转矩阵行列式为|R|=1

（4）每行元素等于其代数余子式

（5）每个元素为变换前后坐标轴夹角的余弦值
易知

$$!\varphi =-arctan(\frac{a_{3}}{c_{3}}),\omega =-arcsin(b_{3}),\kappa =-arctan(\frac{b_{1}}{b_{2}})$$

$$!a_{1}^{2}+a_{2}^{2}+a_{3}^{2}=1,b_{1}^{2}+b_{2}^{2}+b_{3}^{2}=1,c_{1}^{2}+c_{2}^{2}+c_{3}^{2}=1$$

$$!a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}=0,a_{1}c_{1}+a_{2}c_{2}+a_{3}c_{3}=0,b_{1}c_{1}+b_{2}c_{2}+b_{3}c_{3}=0$$

$$!a_{1}^{2}+b_{1}^{2}+c_{1}^{2}=1,a_{2}^{2}+b_{2}^{2}+c_{2}^{2}=1,a_{3}^{2}+b_{3}^{2}+c_{3}^{2}=1$$

$$!a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}=0,a_{1}a_{3}+b_{1}b_{3}+c_{1}c_{3}=0,a_{2}a_{3}+b_{2}b_{3}+c_{2}c_{3}=0$$

像片水平与倾斜像点坐标的关系。（这里，以摄影中心S点为像片旋转中心，因此外方位元素中，主距依旧是f，线元素没有改变）

已知：外方位元素Xs Ys Zs φ ω k(即九个方向余弦)

对于某高程，摄影中心在该高程Z方向的投影N坐标为(Xs,Ys,Zs- $$H_{N}$$ )–物方坐标系

对于某高程，摄影中心在该高程的垂线与像平面的交点n坐标为

$$(-f\frac{c_{1}}{c_{3}},-f\frac{c_{2}}{c_{3}})$$ –像方坐标，可将上点带入共线条件方程后方交会求得↓↓↓

又根据共线方程前方交会公式，在水平图像的平面上，物方任意点A(X,Y,Z)-（物方坐标）在像平面的成像点a为

$$(x^{0},y^{0})$$ -（像平面坐标）或 $$(x^{0},y^{0},-f)$$ 像空间坐标系。↓↓↓

值得注意的是，主光轴正好是垂直于大地水平面，所以，地辅系与像空系只需要在XSY平面上旋转即可。

在倾斜形态中，由像点表示物方点坐标点的公式为：

$$!\frac{X-X_{S}}{Z-Z_{S}}=\frac{a_{1}x+a_{2}y-a_{3}f}{c_{1}x+c_{2}y-c_{3}f}$$

$$!\frac{Y-Y_{S}}{Z-Z_{S}}=\frac{b_{1}x+b_{2}y-b_{3}f}{c_{1}x+c_{2}y-c_{3}f}$$

在垂直形态中，三个角元素严格为0，因次带入之前的矩阵公式得到：

a1=1 a2=0 a3=0 b1=0 b2=1 b3=0 c1=0 c2=0 c3=1

$$!\frac{X-X_{S}}{Z-Z_{S}}=\frac{x^{0}}{-f}$$

$$!\frac{Y-Y_{S}}{Z-Z_{S}}=\frac{y^{0}}{-f}$$

其中

$$x^{0},y^{0}$$ 分别表示水平状态的像点坐标。

上两式的外方位角元素不同，而线元素是相同的。因此联立可得水平纠正的基本公式：

$$!\left\{\begin{matrix}x^{0}=-f\frac{a_{1}x+a_{2}y-a_{3}f}{c_{1}x+c_{2}y-c_{3}f}\\y^{0}=-f\frac{b_{1}x+b_{2}y-b_{3}f}{c_{1}x+c_{2}y-c_{3}f}\end{matrix}\right.$$

 

上文中明确了两个式子：

$$\lbrace \begin{matrix}\frac{f}{\overline{Z}}dXs+\frac{x}{\overline{Z}}dZs-(f+\frac{x^{2}}{f})d\varphi-\frac{xy}{f}d\omega+yd\kappa -\frac{f}{\overline{Z}}dX-\frac{x}{\overline{Z}}dZ+\frac{x}{f}df+dx_{0}-(x-x_{cal})=0 \\\ \frac{f}{\overline{Z}}dYs+\frac{y}{\overline{Z}}dZs -\frac{xy}{f}d\varphi-(f+\frac{x^{2}}{f})d\omega-xd\kappa -\frac{f}{\overline{Z}}dX-\frac{y}{\overline{Z}}dZ+\frac{y}{f}df+dy_{0}-(y-y_{cal})=0 \end{matrix}$$

上式即称为线性化的共线方程。

$$\lbrace \begin{matrix}\frac{f}{\overline{Z}}dXs+\frac{x}{\overline{Z}}dZs-(f+\frac{x^{2}}{f})d\varphi-\frac{xy}{f}d\omega+yd\kappa -\frac{f}{\overline{Z}}dX-\frac{x}{\overline{Z}}dZ+\frac{x}{f}df+dx_{0}-(x-x_{cal})=v_{x}\\\\\frac{f}{\overline{Z}}dYs+\frac{y}{\overline{Z}}dZs -\frac{xy}{f}d\varphi-(f+\frac{x^{2}}{f})d\omega-xd\kappa -\frac{f}{\overline{Z}}dX-\frac{y}{\overline{Z}}dZ+\frac{y}{f}df+dy_{0}-(y-y_{cal})=v_{y}\end{matrix}$$

上式则称为误差方程。

这里面$-(x-x_{cal})$即每一步计算后的值与实际测量值的差，在平差计算过程中，多余的观测数据就是为了进行平差计算获得更精确更均匀的结果。分别命名为$-l_{x}$和$-l_{y}$.一个控制点物方坐标和一个像点坐标组成的两个方程也就有两个误差方程，误差方程的基本公式为

$$V=AX-L$$

有的地方也写为

$$V=A\Delta -L$$

其中V代表误差矩阵，X是待求解的每个元素的改正数矩阵，L是x-x计 y-y计的矩阵。

通常，不会解算物方空间的坐标，同时加入对畸变系数的解算和矫正(将在第四篇提到)，将X分为$X_{in}$、$X_{out}$、$X_{distortion}$，则上式变形为

$$V=AX_{out}+BX_{in}+CX_{distortion}-(xy)_{res}$$

其中，A B C都是各项未知数的系数，$xy_{res}$是像点坐标的误差

$$\lbrace \begin{matrix}x_{res}=x-x_{cal}+x_{dis}\\\\y_{res}=y-y_{cal}+y_{dis}\end{matrix}$$

其中，右边三项分别为像点观测坐标，像点计算坐标，畸变误差。
在后方交会时，当只计算外方位元素时：

$$V_{2n\times 1}=A_{2n\times6}X_{6\times1}-L_{2n\times1}$$ .

其中，式子每两行具体为

$$\begin{bmatrix}v_{x}\\\\v_{y}\end{bmatrix}=\begin{bmatrix}\frac{f}{\overline{Z}}&0&\frac{x}{\overline{Z}}&-(f+\frac{x^{2}}{f})&-\frac{xy}{f}&y\\\\0&\frac{f}{\overline{Z}}&\frac{y}{\overline{Z}}&-\frac{xy}{f}&-(f+\frac{y^{2}}{f})&-x\end{bmatrix}\begin{bmatrix}dXs\\\\dYs\\\\dZs\\\\d\varphi\\\\d\omega\\\\d\kappa\end{bmatrix}-\begin{bmatrix}l_{x}\\\\l_{y}\end{bmatrix}$$

若要求出V方程的最佳估计值，在摄影测量中，一般按照最小二乘原理进行解答，即

$$V^{T}V=min$$ 这就转化为了对该式求极值的问题。

$$V^{T}V=(AX-L)^{T}(AX-L)=X^{T}A^{T}AX-2X^{T}A^{T}L+L^{T}L\Rightarrow \frac{\partial V^{T}V}{\partial X}=2A^{T}AX-2A^{T}L=0$$

上式中大X的含义是待求解的每个元素的残差矩阵包含了Xs Ys Zs Ω φ k，而不是实际测量三维点坐标X。此外，推导过程中对$V^{T}V$求导，则可得到对应6个残差的最佳估计值。这个过程称为误差方程式的法化。

上式整理后可得

$$A^{T}AX-A^{T}L=A^{T}(AX-L)=0$$

有的地方亦写作

$$A^{T}P(A\Delta -L)=0$$ Δ与X同含义，而P是测量平差中进行稳健估计而使用的权矩阵，即
$$\begin{bmatrix}P_{1}&&&&&\\&P_{2}&&&&\\&&.&&&\\&&&.&&\\&&&&.&\\&&&&&P_{n}\end{bmatrix}$$
非主要内容略微说一下测量平差的估值。主要目的是处理含有误差（其中一些误差可能较大，定义为比最大偶然误差还要大的误差，称为粗差）依赖一定的数学模型，包含函数模型和随即模型，按照某种估计准则，求出未知参数的最优估值，并评定其精度。当粗差归为函数模型，粗差表现为观测量误差绝对值较大且偏离群体，处理思想是在正式进行最小二乘平差之前探测和定位粗差，然后剔除含有粗差的观测值，得到一组比较净化的观测值，模型为均值漂移模型；将粗差归为随机模型，粗差即表现为先验随机模型和实际随机模型的差异过大，处理方法为根据逐次迭代平差的结果不断地改变观测值的权或者方差，最终使粗差观测值的权趋于零或者方差趋于无穷大，模型为方差膨胀模型。

该方法的实践逻辑是由于不大准确知道观测数据中有效信息和有害信息所占的比例及其它们具体包含在哪些观测中，要冒着损失一些效率的风险，去获得较可靠的、具有实际意义的、较有效的估值。针对极大似然估计的稳健估计模型主要使用M估计。而M估计应用最广的是选权迭代法。而P可以使等权独立观测的P=I，也可以是权函数矩阵代替观测权阵P。这里不展开来讲。

法化后的方程称为法方程式，一般写作

$$NX=A^{T}L$$ ,其中$N=A^{T}A$也把N称为法方程的系数。

上两式就是法方程，也是△Xs，△Ys，△Zs，△k，△φ，△ω的解。

答解改正数： $$X=(A^{T}A)^{-1}A^{T}L$$ 或 $$\Delta =(A^{T}PA)^{-1}A^{T}PL$$

计算每一步迭代值： $$X_{s}^{k+1}=X_{s}^{k}+dXs^{k+1},Y_{s}^{k+1}=Y_{s}^{k}+dYs^{k+1},Z_{s}^{k+1}=Z_{s}^{k}+dZs^{k+1}$$
$$\varphi ^{k+1}=\varphi ^{k}+d\varphi ^{k+1},\omega ^{k+1}=\omega ^{k}+d\omega ^{k+1},\kappa ^{k+1}=\kappa ^{k}+d\kappa ^{k+1}$$

这里注意，平坦地区不适宜内外元素同时答解，因为dXs0与dx0相关，dYs0与dy0相关。

空间后方交会的平面二维坐标的选点，应尽可能的布满整个区域。或者覆盖中心和边缘的更全面的位置，如图。不均匀以及不足够数量的控制点参与迭代会极大的影响最终计算的精度。



具体的迭代流程如下：

①确定各未知数的初值$X_{s}^{0},Y_{s}^{0},Z_{s}^{0},\varphi ^{0},\omega ^{0},\kappa ^{0}$
②对每个控制点计算误差方程系数aij和lx、ly。按照最上面的公式列出误差方程。
③答解线性方程组，得到△Xs，△Ys，△Zs，△k，△ω，△φ

④将增量△和初值相加，得到新的一个外方位元素。

⑤各个增量△与一个给定的限差作比较，若小于则停止迭代运算；若不是则重复②到⑤
​
分别对上式各步骤进行解释：
①$X_{s}^{0},Y_{s}^{0}$可以利用X Y的物方点均值设置，$Z_{s}^{0}$一般为H即航摄高度，有时也用mf表示。m是航摄比例尺，f是相机焦距。这些值也可以直接给定某个初值。三个角元素则一般设为0,k有时可根据航迹图给定。

②该步骤可分解为计算旋转矩阵R（R的具体值参考下文）、计算得到的变换坐标$\overline{X},\overline{Y},\overline{Z}$（其实就是地面辅助坐标系的坐标）、计算x计、y计（即由相应地面坐标点和外方位元素计算得到的像点坐标，

$$x_{cal}=-f\frac{\overline{X}}{\overline{Z}},y_{cal}=-f\frac{\overline{Y}}{\overline{Z}}$$ 、计算误差方程各项系数、组成误差方程V=AX-L

③该步骤其实就是矩阵运算，求出$A^{T}PA$ ($A^{T}A$) 及其逆矩阵。求出$A^{T}L$ ($A^{T}PL$)，两式相乘求取X[△Xs,△Ys,△Zs,△k,△ω,△φ]

④根据改正数的值加上上一步的值得到各项新值。

⑤检查是否收敛时，一般只对角元素改正数设定限差，为0.1’（按弧度值是0.0000291rad）当三个角改正数都小于限差时迭代结束。
平差理论中，单位权中的误差为

$$m_{0}=\sqrt{\frac{\sum v_{i}^{2}}{2n-t}}​$$ 其中m0为单位权中误差。vi是第i个方程的残差，n是控制点个数，t是未知数个数。只解求外方位精度则只有6个精度。

根据传播定律，

$$m^{2}=N^{-1}m_{0}^{2}$$ 式中$N^{-1}$是法方程系数矩阵的逆矩阵。即

$$N^{-1}=\begin{bmatrix}Q_{11}&Q_{12}&.&.&.&Q_{1t}\\Q_{21}&Q_{22}&.&.&.&Q_{2t} \\\ .&.&.&.&.&.\\\ .&.&.&.&.&.\\\ .&.&.&.&.&.\\Q_{t1}&Q_{t2}&.&.&.&Q_{tt}\end{bmatrix}$$ ,则第i个未知数中的误差为:

$m_{i}=\sqrt{Q_{ii}}m_{0}$,其中$Q_{ii}$为$N^{-1}$的各项系数的对角元素,也称为第i个未知数的权倒数。

——一点说明

再次声明，无论半片还是全片，增加控制点都可以提高精度，但精度提高的不是很大；采用相同数量控制点，全片比半片精度成倍的提高，分布良好更有利于精度改善。

各种文档看得累。条理不清结构不明缺斤少两。决定自己总结一个。（公式较多，墙外浏览更顺哟）

一些注意

后方交会是为了获取影像的内外方位数据，其中外方位数据可以通过GPS、INS（惯性导航系统）、雷达、星相摄像机来获取；然而由于穷穷穷，只能利用影响覆盖范围内的一定控制点来计算空间坐标与影响坐标之间的关系，来反算外方位元素。 多片检校基于单片检校。在矩阵组合时分别解算外方位元素。但使用同一组内方位元素。在一个大矩阵内进行。
后方交会可以只检校外方位元素。当需要进行畸变差校正时（即畸变差不可忽略时），可在方程中加入畸变差项进行迭代；当需要进行内方位元素检校时（即内方位元素精度没有达到需求），可在方程中加入内方位元素进行迭代。 对于畸变差校正，包括径向畸变、切向畸变、薄棱镜畸变，其中多数情况考察径向畸变的前两项系数k1 k2和切向畸变p1 p2 ，在某些组合相机的畸变模型中，还包括α像素非正方形比例和βccd非正交性畸变系数。
对于内方位元素检校，有的地方将f分为fx和fy即f在坐标两个方向上的像素值（由于有的xy不是同一比例尺即不是正方形） 检校，就是纠正相机各个方面的误差和精度，可以得到相机内部的主点、焦距、畸变的客观信息，这些信息在大部分情况下不会轻易改变；而相机外部的空间位置时时刻刻都在改变，但一些论文指出，在焦距变化、空间位置变化、移轴、高空拍摄情况下，相机的焦距、主点位置也会随之或多或少的改变，因此迭代时最好能带上这些参数一起进行平差。

一些重要概念
后方交会基于共线方程，物理含义为同一个三维坐标系中投影中心、物方点、像平面投影的点在同一条直线上。

$$x-x_{0}=-f\cdot \frac{a_{1}(X-X_{s})+b_{1}(Y-Y_{s})+c_{1}(Z-Z_{s})}{a_{3}(X-X_{s})+b_{3}(Y-Y_{s})+c_{3}(Z-Z_{s})}$$

$$y-y_{0}=-f\cdot \frac{a_{2}(X-X_{s})+b_{2}(Y-Y_{s})+c_{2}(Z-Z_{s})}{a_{3}(X-X_{s})+b_{3}(Y-Y_{s})+c_{3}(Z-Z_{s})}$$

上式中，包含留个外方位元素，即Xs、Ys、Zs、φ、Ω、k。只有确定了六个外方位元素，才能确定摄影中心在物方空间的位置。a1、a2、a3、b1、b2、b3、c1、c2、c3是需要计算的直线方程的系数，其物理性质是3个外方位角元素组成的9个方向余弦。该方程利用了相似三角形的性质；f是焦距长，X Y Z均值控制点的测量坐标，默认为精确的，因此物方控制点测量的精度很大程度上决定了最后检校的精度；x y是X Y Z对应的像平面的坐标，x0，y0是主点在像平面的坐标，有时当作已知并不再改变，有时也参与迭代计算。

共线条件方程用途有：

1. 单像、多像空间后方交会；多像空间前方交会
2. 解析空中三角测量的光束法平差
3. 数字投影的基础
4. 计算模拟影像数据（已知内外方位元素和物方坐标点求像点）
5. DEM与共线方程制作正射影像
6. DEM与共线方程进行单幅影像测图

注意 一个方程代表一个点在像平面和物方世界的关系，因此一个点对应两个方程，若有n个控制点，则对应2n个方程

若f x0 y0当作已知，则有外方位元素6个未知数，因此需要6个方程，即3个控制点的方程；若f x0 y0当作未知，则有9个未知数，因此需要至少5个控制点的方程。当然，很多文章也指出，越多的冗余数据参与计算得到的结果也越精确；越多的像片参与计算，得到的结果越精确；更均匀的控制点分布，能更多的控制整张像片，均匀的分布在边缘，得到的结果更精确。

一般情况下，令

$$\overline{X}=a_{1}(X-X_{s})+b_{1}(Y-Y_{s})+c_{1}(Z-Z_{s})$$

$$\overline{Y}=a_{2}(X-X_{s})+b_{2}(Y-Y_{s})+c_{2}(Z-Z_{s})$$

$$\overline{Z}=a_{3}(X-X_{s})+b_{3}(Y-Y_{s})+c_{3}(Z-Z_{s})$$

而用矩阵的形式可以表示为：

$$\begin{pmatrix}\overline{X}\\\overline{Y}\\\overline{Z}\end{pmatrix}=\begin{pmatrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\a_{3}&b_{3}&c_{3}\end{pmatrix}\cdot\begin{pmatrix}X-Xs\\Y-Ys\\Z-Zs\end{pmatrix}=R^{T}\begin{pmatrix}X-Xs\\Y-Ys\\Z-Zs\end{pmatrix}$$

这里R是旋转矩阵，且$R^{T}=R^{-1}$,行列式的值为0，即任意元素等于其代数余子式的值.则共线方程变为：

$$x-x_{0}=-f\cdot \frac{\overline{X}}{\overline{Z}},y-y_{0}=-f\cdot \frac{\overline{Y}}{\overline{Z}}$$

由于上式是共线方程的变形，因此Fx和Fy是六个外方位元素为参数的函数。由于方程是非线性的，因此不能解求数值，需要对方程进行线性化。思路是，对上式按泰勒级数在初值处展开并保留一次项，将非线性方程转化为各参数改正数的线性方程

设初值为

$$X_{S}^{0},X_{S}^{0},Z_{S}^{0},\varphi^{0},\omega^{0},\kappa {0},X^{0},Y^{0},Z^{0},x_{0}^{0},y_{0}^{0},f^{0}$$

相应的改正数为

$$dXs=\triangle Xs=Xs-Xs^{0},dYs=\triangle Ys=Ys-Ys^{0},dZs=\triangle Zs=Zs-Zs^{0}$$

$$d\varphi=\triangle \varphi=\varphi-\varphi^{0},d\omega=\triangle \omega=\omega-\omega^{0},d\kappa=\triangle \kappa=\kappa-\kappa^{0}$$

$$dX=\triangle X=X-X^{0},dY=\triangle Y=Y-Y^{0},dZ=\triangle Z=Z-Z^{0}$$

 则共线方程的泰勒一次展开一般式为①

$$x=(x)+\frac{\partial x}{\partial Xs}dXs+\frac{\partial x}{\partial Ys}dYs+\frac{\partial x}{\partial Zs}dZs+\frac{\partial x}{\partial \varphi }d\varphi +\frac{\partial x}{\partial \omega }d\omega +\frac{\partial x}{\partial \kappa }d\kappa +\frac{\partial x}{\partial X}dX+\frac{\partial x}{\partial Y}dY+\frac{\partial x}{\partial x_{0}}dx_{0}+\frac{\partial x}{\partial y_{0}}dy_{0}+\frac{\partial x}{\partial f}df$$

$$y=(y)+\frac{\partial y}{\partial Xs}dXs+\frac{\partial y}{\partial Ys}dYs+\frac{\partial y}{\partial Zs}dZs+\frac{\partial y}{\partial \varphi }d\varphi +\frac{\partial y}{\partial \omega }d\omega +\frac{\partial y}{\partial \kappa }d\kappa +\frac{\partial y}{\partial X}dX+\frac{\partial y}{\partial Y}dY+\frac{\partial y}{\partial x_{0}}dx_{0}+\frac{\partial y}{\partial y_{0}}dy_{0}+\frac{\partial y}{\partial f}df$$

这是一个重要的总结性公式。(x)(y)分别是内方位元素x，y的初值。式中包含了所有内外元素和物放测量点。当进行不同矩阵运算时，可以选择需要的精度不足够的进行迭代计算。

其中，对x和y求各未知项的偏导：

$$\frac{\partial x}{\partial Xs}=-f\cdot \frac{\frac{\partial \overline{X}}{\partial Xs}\overline{Z}-\frac{\partial \overline{Z}}{\partial Xs}\overline{X}}{\overline{Z}^{2}}=-\frac{f}{\overline{Z}^{2}}(-a_{1}\overline{Z}+a_{3}\overline{X})=\frac{1}{\overline{Z}}[a_{1}f-a_{3}f\frac{\overline{X}}{\overline{Z}}]=\frac{1}{\overline{Z}}[a_{1}f+a_{3}(x-x_{0})]$$

同理，其他的偏导为

$$\begin{align} \frac{\partial x}{\partial Ys} & =\frac{1}{\overline{Z}}[b_{1}f+b_{3}(x-x_{0})] \\ \frac{\partial x}{\partial Zs} & =\frac{1}{\overline{Z}}[c_{1}f+b_{3}(x-x_{0})] \\ \frac{\partial y}{\partial Xs} & =\frac{1}{\overline{Z}}[a_{2}f+a_{3}(x-x_{0})] \\ \frac{\partial y}{\partial Ys} & =\frac{1}{\overline{Z}}[b_{2}f+b_{3}(x-x_{0})] \\ \frac{\partial y}{\partial Zs} & = \frac{1}{\overline{Z}}[c_{2}f+c_{3}(x-x_{0})] \\ \frac{\partial x}{\partial f} & =\frac{x-x_{0}}{f}=-\frac{\overline{X}}{\overline{Z}} \\ \frac{\partial y}{\partial f} & =\frac{y-y_{0}}{f}=-\frac{\overline{Y}}{\overline{Z}} \\ \frac{\partial x}{\partial x_{0}} & =1,\frac{\partial x}{\partial y_{0}}=0\\ \frac{\partial y}{\partial x_{0}} & =0,\frac{\partial y}{\partial y_{0}}=1 \end{align}$$

这里相对比较难解决的是角元素的偏导，关于角度的问题可以参考第三篇。

角度的变换在这里不再详述，两个坐标系之间的转换可以归结为变换矩阵的求取。三个角元素共同构成了矩阵的元素确定。 由于

$$R^{T}=R_{\kappa }^{T}R_{\omega }^{T}R_{\varphi }^{T}$$

因而，难度转到求取$\overline{X}\overline{Y} \overline{Z}$对角元素的偏导上。对角元素求偏导可以分为三个步骤：

①求各个方向余弦$a_{i},b_{i},c_{i}$对ω、k、φ的偏导数。共27个。

②求$\overline{X},\overline{Y},\overline{Z}$对ω、k、φ的偏导数，共9个。

③求x、y对ω、k、φ的偏导数，共6个。

如下是$\overline{X},\overline{Y},\overline{Z}$对φ的偏导，三个参数写在矩阵中，有的地方也展开写成每一项的等式形式。

$$\begin{align} \frac{\partial }{\partial \varphi }\begin{pmatrix}\overline{X}\\\overline{Y}\\\overline{Z}\end{pmatrix}&=R_{\kappa }^{T}R_{\omega }^{T}\frac{\partial R_{\varphi }^{T}}{\partial \varphi }\begin{pmatrix}X-Xs\ Y-Ys\ Z-Zs\end{pmatrix}=R_{\kappa }^{T}R_{\omega }^{T}\frac{\partial R_{\varphi }^{T}}{\partial \varphi }(R^{T})^{-1}\begin{pmatrix}\overline{X}\ \overline{Y}\ \overline{Z}\end{pmatrix}=R_{\kappa }^{T}R_{\omega }^{T}\frac{\partial R_{\varphi }^{T}}{\partial \varphi }R\begin{pmatrix}\overline{X}\ \overline{Y}\ \overline{Z}\end{pmatrix}\\\ &=R_{\kappa }^{T}R_{\omega }^{T}(R_{\varphi }^{T}R_{\varphi })\frac{\partial R_{\varphi }^{T}}{\partial \varphi }R\begin{pmatrix}\overline{X}\ \overline{Y}\ \overline{Z}\end{pmatrix}=R^{T}R_{\varphi }\frac{\partial R_{\varphi }^{T}}{\partial \varphi }R\begin{pmatrix}\overline{X}\ \overline{Y}\ \overline{Z}\end{pmatrix} \end{align}$$

带入具体系数，上式可变形为

$$\begin{matrix} \begin{pmatrix}a_{1} & b_{1} & c_{1}\\a_{2} & b_{2} & c_{2}\\a_{3} & b_{3} & c_{3}\end{pmatrix}\begin{pmatrix}0 & 0 &1\\0 & 0 & 0\\\ -1 & 0 & 0\end{pmatrix}\begin{pmatrix}a_{1} & a_{2} & a_{3}\\b_{1} & b_{2} & b_{3}\\c_{1} & c_{2}&c_{3} \end{pmatrix}\begin{pmatrix}\overline{X}\\\overline{Y}\\\overline{Z} \end{pmatrix}\\ =\begin{pmatrix}0 &-a_{2}c_{1}+a_{1}c_{2}&-a_{3}c_{1}+a_{1}c_{3}\\\ -a_{1}c_{2}+a_{2}c_{1} & 0 & -a_{3}c_{2}+a_{2}c_{3}\\\ -a_{1}c_{3}+a_{3}c_{1}& -a_{2}c_{3}+a_{3}c_{2} &0\end{pmatrix}\begin{pmatrix}\overline{X}\\\overline{Y}\\\overline{Z} \end{pmatrix} \\ = \begin{pmatrix}0 & -b_{3} & b_{2}\\b_{3}&0&-b_{1}\\\ -b_{2}&b_{1}&0\end{pmatrix}\begin{pmatrix}\overline{X}\\\overline{Y}\\\overline{Z} \end{pmatrix} \end{matrix}$$
其中利用了旋转矩阵一个元素的值等于代数余子式的值。如下是$\overline{X},\overline{Y},\overline{Z}$对ω的偏导。

$$\begin{align} \frac{\partial }{\partial \omega }\begin{pmatrix}\overline{X}\\\overline{Y}\\\overline{Z}\end{pmatrix} &=R_{\kappa }^{T}\frac{\partial R_{\omega}^{T}}{\partial \omega }R_{\varphi }^{T}\begin{pmatrix}X-Xs\\Y-Ys\\Z-Zs\end{pmatrix}=R_{\kappa}^{T}\frac{\partial R_{\omega }^{T}}{\partial \omega }R_{\varphi }^{T}(R_{\varphi }R_{\omega }R_{\kappa })\begin{pmatrix}\overline{X}\\\overline{Y}\\\overline{Z}\end{pmatrix}\\ &=R_{\kappa }^{T}\frac{\partial R_{\omega }^{T}}{\partial \omega}R_{\omega }R_{\kappa }\begin{pmatrix}\overline{X}\ \overline{Y}\ \overline{Z}\end{pmatrix}= \begin{pmatrix}0&0&sin\kappa\\\ 0&0&cos\kappa \\\ -sin\kappa&-cos \kappa&0\end{pmatrix}\begin{pmatrix}\overline{X}\ \overline{Y}\ \overline{Z}\end{pmatrix} \end{align}$$ 其中，这里用到了

$$\begin{pmatrix}\overline{X}\\\overline{Y}\\\overline{Z}\end{pmatrix}=R^{T}\begin{pmatrix}X-Xs\\Y-Ys\\Z-Zs\end{pmatrix}=(R_{\varphi}R_{\omega}R_{\kappa })^{T}\begin{pmatrix}X-Xs\\Y-Ys\\Z-Zs\end{pmatrix}=R_{\kappa }^{T}R_{\omega }^{T}R_{\varphi }^{T}\begin{pmatrix}X-Xs\\Y-Ys\\Z-Zs\end{pmatrix}$$

$$\begin{pmatrix}X-Xs\\Y-Ys\\Z-Zs\end{pmatrix}=(R^{T})^{-1}\begin{pmatrix}\overline{X}\\\overline{Y}\\\overline{Z}\end{pmatrix}=R\begin{pmatrix}\overline{X}\\\overline{Y}\\\overline{Z}\end{pmatrix}=R_{\varphi }R_{\omega }R_{\kappa }\begin{pmatrix}\overline{X}\\\overline{Y}\\\overline{Z}\end{pmatrix}$$

如下是$\overline{X},\overline{Y},\overline{Z}$对k的偏导。

$$\begin{align} \frac{\partial }{\partial \kappa }\begin{pmatrix}\overline{X}\ \overline{Y}\ \overline{Z}\end{pmatrix}&=\frac{\partial R_{\kappa }^{T}}{\partial \kappa }R_{\omega }^{T}R_{\varphi }^{T}\begin{pmatrix}X-Xs\\Y-Ys\\Z-Zs\end{pmatrix}\\&=\frac{\partial R_{\kappa }^{T}}{\partial \kappa }(R_{\kappa }R_{\kappa }^{T})R_{\omega }^{T}R_{\varphi }^{T}\begin{pmatrix}X-Xs\\Y-Ys\\Z-Zs\end{pmatrix}\\ &=\frac{\partial R_{\kappa }^{T}}{\partial \kappa }R_{\kappa }\begin{pmatrix}\overline{X}\ \overline{Y}\ \overline{Z}\end{pmatrix}=\begin{pmatrix}\overline{Y} \\\- \overline{X}\\0\end{pmatrix} \end{align}$$
通过以上三式可得到x和y对各角元素未知数的偏导。有的地方，将x，y先分别除以$\overline{Z}$,这样可以在求取偏导的时候减少计算量。
$$\begin{align} \frac{\partial x}{\partial \varphi} & = -\frac{f}{\overline{Z}^{2}}(\frac{\partial \overline{X}}{\partial \varphi }\overline{Z}-\frac{\partial \overline{Z}}{\partial \varphi }\overline{X}) \\ & = -\frac{f}{\overline{Z}^{2}}(-b_{3}\overline{Y}+b_{2}\overline{Z})\overline{Z}+\frac{f}{\overline{Z}^{2}}(b_{2}\overline{X}-b_{1}\overline{Y})\overline{X} \\ & = -(y-y_{0})b_{3}-fb_{2}-\frac{(x-x_{0})^{2}}{f}b_{2}+\frac{(x-x_{0})(y-y_{0})}{f}b_{1} \\ & = \frac{(x-x_{0})(y-y_{0})}{f}b_{1}-(f+\frac{(x-x_{0})^{2}}{f})b_{2}-(y-y_{0})b_{3} \end{align}$$
其他以此类推
$$\begin{align} \frac{\partial x}{\partial \omega } &= \frac{(x-x_{0})^{2}}{f}sin\kappa-\frac{(x-x_{0})(y-y_{0})}{f}cos\kappa -fsin\kappa \\\ \frac{\partial x}{\partial \kappa } &= (f+\frac{(y-y_{0}^{2})}{f})b_{1}-\frac{(x-x_{0})(y-y_{0})}{f}b_{2}-(x-x_{0})b_{3} \\ \frac{\partial y}{\partial \omega } &= -\frac{(x-x_{0})(y-y_{0})}{f}sin\kappa -\frac{(y-y_{0})^{2}}{f}cos\kappa -fcos\kappa \\ \frac{\partial y}{\partial \kappa }&=-(x-x_{0}) \end{align}$$
以上求出了所有的偏导，则①式的公式可变为更重要的式②

$$\begin{aligned} c_{11}dXs+c_{12}dYs+c_{13}dZs+c_{14}d\phi +c_{15}d\omega &+c_{16}d\kappa \\\ -c_{11}dX &-c_{12}dY-c_{13}dZ+c_{17}df+c_{18}dx_{0}+c_{19}dy_{0}-lx=0 \end{aligned}$$
$$\begin{aligned} c_{21}dXs+c_{22}dYs+c_{23}dZs+c_{24}d\phi +c_{25}d\omega &+c_{26}d\kappa \\\ -c_{21}dX &-c_{22}dY-c_{23}dZ+c_{27}df+c_{28}dx_{0}+c_{29}dy_{0}-ly=0 \end{aligned}$$
这里可以看到，Xs和X Ys和Y Zs和Z的偏导互为相反数，因此12个未知数只需要求解9个。 其中c的系数分别为：
$$\begin{align} c_{11}& = \frac{1}{\overline{Z}}(a_{1}f+a_{3}(x-x_{0})) \\ c_{12}& = \frac{1}{\overline{Z}}(b_{1}f+b_{3}(x-x_{0})) \\ c_{13}& = \frac{1}{\overline{Z}}(c_{1}f+c_{3}(x-x_{0})) \\ c_{14}& = \frac{(x-x_{0})(y-y_{0})}{f}b_{1}-(f+\frac{(x-x_{0})^{2}}{f})b_{2}-(y-y_{0})b_{3} \\ c_{15}& = -\frac{(x-x_{0})^{2}}{f}sin\kappa -\frac{(x-x_{0})(y-y_{0})}{f}cos\kappa -fsin\kappa \\ c_{16}& = y-y_{0}\\ c_{17}& = \frac{x-x_{0}}{f},c_{18}=1,c_{19}=0,lx=x-x_{cal}\\ c_{21} &= \frac{1}{\overline{Z}}(a_{2}f+a_{3}(y-y_{0}))\\ c_{22} &= \frac{1}{\overline{Z}}(b_{2}f+b_{3}(y-y_{0}))\\ c_{23} &= \frac{1}{\overline{Z}}(c_{2}f+c_{3}(y-y_{0}))\\ c_{24} &= (f+\frac{(y-y_{0})^{2}}{f})b_{1}-\frac{(x-x_{0})(y-y_{0})}{f}b_{2}+(x-x_{0})b_{3}\\ c_{25} &= -\frac{(x-x_{0})(y-y_{0})}{f}sin\kappa -\frac{(y-y_{0})^{2}}{f}cos\kappa -fcos\kappa \\ c_{26} &= -(x-x_{0})\\ c_{27}&=\frac{y-y_{0}}{f},c_{28}=0,c_{29}=1,ly=y-y_{cal}\end{align}$$

在正摄影像近似垂直时，可以采用φ≈ω≈k≈0,$\overline{Z}\approx -H$的取值带入系数中，则②式可化简为本篇最终的结果式③：

$$\left\{\begin{matrix}v_{x}=-\frac{f}{H}dXs-\frac{x-x_{0}}{H}dZs-[f+\frac{(x-x_{0})^{2}}{f}]d\varphi-\frac{(x-x_{0})(y-y_{0})}{f}d\omega+(y-y_{0})d\kappa+\frac{f}{H}dX+\frac{x-x_{0}}{H}dZ+\frac{x-x_{0}}{f}df+dx_{0}-(x-x_{cal})\\v_{y}=-\frac{f}{H}dYs-\frac{y-y_{0}}{H}dZs-\frac{(x-x_{0})(y-y_{0})}{f}d\varphi-[f+\frac{(y-y_{0})^{2}}{f}]d\omega+(x-x_{0})d\kappa+\frac{f}{H}dY+\frac{y-y_{0}}{H}dZ+\frac{y-y_{0}}{f}df+dy_{0}-(y-y_{cal})\end{matrix}\right.$$

式中相对①式添加了改正项，为了平衡一次项以下的展开式对结果的影响，是平差方程中重要的一部。误差方程将在下文提到。

在 2015 年这一年，这种从相杀到相爱的事情已经发生了三次：
2015 年 2 月 14 日，滴滴和快的宣布合并；
2015 年 4 月 17 日，58 与赶集宣布合并；
2015 年 10 月 8 日，美团与大众点评宣布合并。

分享一个装机清单。

今天。听李志和陈粒

基于上回对Harris的角点检测和匹配的过程，试想这学习一下另一种角点检测和匹配算法sift.
在《Python计算机视觉》书中，由于Python实现所有步骤的效率并不是很高，提到了VLFeat工具进行SIFT兴趣点的检测。

好的，那就去官网找。它明确写着Windows Mac Linux都可用。太好了。但是主要提供的是c 和 MATLAB 的api，在python中只能利用shell进行接口的调用。将目录下的\bin\arch\sift.exe 添加到path环境路径，就能在cmd控制台使用shell。可是测试了几次，依据例子或者普林斯顿的抄袭版本，都只能打开可视化的界面，不能输入需要的.sift或者frame图像。

好吧换个方案，听说Python有一个包装器。找到了供github下的pyhton wrappers主页（居然是寄生在MATLAB的插件下面）可是。。可是。在它的readme发现只能在linux和Mac OX使用。。书中亦提到包装器的安装需要非常高的技巧。好吧放弃。

再次寻找。发现一个python官网提供的一个python插件。直接可以利用setup.py insatll进行安装。好了进行安装

python setup.py install

居然出现了bug

Unable to find vcvarsall.bat

找到一些讨论，大家都说是要安MinGW，找到它的官网，这个看起来不错。默认选择了安装路径，又安装了一堆.bin 的类库。输入

setup.py install build --compiler=mingw32

又出现了bug

error: numpy/arrayobject.h: No such file or directory

日了狗了。在这里说需要加点什么路径，然后又在这里发现了说是它的mingw已经很旧了不太能匹配新的版本的软件了。可以找到一个非官方版本。

好吧。开心的安上。再一次安了gcc等一系列乱七八糟的bin库。然后执行。。。shit。又是bug arraypobjects.h又找不到。。

好吧超出了我的技能点了。顺带在半路还捡到一个非官方的python类库，叫做unofficial windows binaries for python extention package
..

正在绝望之时。。居然在csdn发现了这本书的源代码oh wtf。居然它的自带vlfeat能用。好吧到此结束了。直接用命令行好了。py中利用

os.system('cmd')

使用命令行进行编写。

最近学习计算机视觉，初步学习了特征点的几个算子和描述子，最初级的是Harris和进阶的SIFT.囿于最近又想学python所以弄了一下它的数值计算的库scipy numpy和图形界面的库PIL和matplotlib..具体环境是：

1. 1python环境的搭建有两种方式，可以使用官方的Python2.79 搭配上Enthought提供的一个轻量Free版本canopy供学习和开发者使用（包括NumPy, SciPy, Pandas, Matplotlib, IPython）；或者直接使用Scipy官网推荐使用的Python其他搭载了Numpu和Scipy的发行版，我体验了Python(x,y)效果还是不错的
2. PIL图像库，可在其官网下载最新版本1.1.7的PIL（虽然已经是2009年。。目前只支持2.X可在WIn LInux OX平台使用）
3. Matplotlib在安装Numpy和Scipy时应该已经提供，若没有下载完成则可在其网站免费获取

Harris特征检测

安装完成后就可以进行Python图形可视化的编写。首先对Harris角点检测算法有个介绍。主要思想是，如果像素周围存在多于一个方向的边，认为该点就是兴趣点，称为角点。

角点的定义是：局部窗口沿各方向运动，均产生明显变化的点；图像局部曲率突变的点。窗口函数可以选择创体内1窗体外0，或者高斯函数。窗口移动导致的图像变化可利用实对称矩阵的特征值分析，计算各角点的响应。其中一种方式是，利用最大的特征值进行判断，对特征值均非常大的，表述为各方向上变化均非常大；对特征值均非常小的，表述为各方向上无明显变化；若一个特征值大一个特征值小，则判定为边缘。另一种方法是，利用响应函数det (H)−αtrace(H)^2 或者λ0λ1/(λ0+λ1)。最后，利用阈值筛选出局部极大值。该算法具有光照不变性，旋转不变性，对比度部分不变。尺度变换不具有不变性。

from scipy.ndimage import filters
from PIL import Image
from numpy import *
from pylab import *

def compute_harris_response(im,sigma=3):
#计算harris响应函数
imx = zeros(im.shape)
filters.gaussian_filter(im,(sigma,sigma),(0,1),imx)
imy = zeros(im.shape)
filters.gaussian_filter(im,(sigma,sigma),(1,0),imy)

Wxx = filters.gaussian_filter(imx*imx,sigma)
Wxy = filters.gaussian_filter(imx*imy,sigma)
Wyy = filters.gaussian_filter(imy*imy,sigma)

Wdet = Wxx*Wyy - Wxy**2
Wtr = Wxx +Wyy

return Wdet / Wtr

def get_harris_points(harrisim,min_dist,threshold):

corner_threshold = harrisim.max() * threshold
harrisim_t = (harrisim > corner_threshold) * 1

coords =array(harrisim_t.nonzero()).T

candidate_values = [harrisim[c[0],c[1]] for c in coords]

index = argsort(candidate_values)

allowed_locations = zeros(harrisim.shape)
allowed_locations[min_dist:-min_dist,min_dist:-min_dist]=1

filtered_coords = []
for i in index:
if allowed_locations[coords[i,0],coords[i,1]] == 1:
filtered_coords.append(coords[i])
allowed_locations[(coords[i,0]-min_dist):(coords[i,0]+min_dist),(coords[i,1]-min_dist):(coords[i,1]+min_dist)] = 0
return filtered_coords

def plot_harris_points(im1,im2,filtered_coords1,filtered_coords2):
figure()
gray()
im=concatenate((im1,im2),axis=1)
imshow(im)
shp1 = im1.shape[1]
for j in filtered_coords2:
jj = [j[0] , j[1] +shp1]
filtered_coords1.append(jj)
plot([p[1] for p in filtered_coords1],[p[0] for p in filtered_coords1],'*')
axis('off')
show()

im01= array(Image.open('1.JPG'))
im02= array(Image.open('2.JPG'))
im1 = array(Image.open('1.JPG').convert('L'))
im2 = array(Image.open('2.JPG').convert('L'))
harrisim1 = compute_harris_response(im1)
harrisim2 = compute_harris_response(im2)
min_dist=7
threshold=0.05
filtered_coords1 = get_harris_points(harrisim1,min_dist,threshold)
filtered_coords2 = get_harris_points(harrisim2,min_dist,threshold)
print len(filtered_coords1)
print len(filtered_coords2)
plot_harris_points(im01,im02,filtered_coords1,filtered_coords2)

其中1.jpg和2.jpg可换成自己的图像。函数说明在注释中已说明。

##

harris特征匹配

角点检测器只能检测图像中的兴趣点，但是没有给出匹配角点的方法，这里需要对每个角点加上描述子信息，即角点周围的点的信息。描述子描述越好，寻找匹配对应点越好。Harris角点的描述子又周围像素块的灰度值以及用于比较归一化互相关矩阵构成。通常两个相同大小像素块的相关矩阵定义为函数f对像素块卷积的和。归一化互相关矩阵的一种变形可以定义为：

其中，n表示像素块的数目，μ1和μ2表示每个像素块平均像素强度，σ1和σ2表示每个像素块的标准差。通过减去均值和标准差，该方法对图像亮度变化具有稳健性。

#_*_encoding:utf-8_*_
from scipy.ndimage import filters
from PIL import Image
from numpy import *
from pylab import *</code>

def compute_harris_response(im,sigma=3):
#计算灰度图像中harris角点响应函数

#计算导数
imx = zeros(im.shape)
filters.gaussian_filter(im,(sigma,sigma),(0,1),imx)
imy = zeros(im.shape)
filters.gaussian_filter(im,(sigma,sigma),(1,0),imy)
#计算harris矩阵分量
Wxx = filters.gaussian_filter(imx*imx,sigma)
Wxy = filters.gaussian_filter(imx*imy,sigma)
Wyy = filters.gaussian_filter(imy*imy,sigma)
#计算特征值和迹
Wdet = Wxx*Wyy - Wxy**2
Wtr = Wxx +Wyy

return Wdet / Wtr

def get_harris_points(harrisim,min_dist,threshold):
#得到harris特征点集 harrisim是计算harris响应函数的灰度图像 min_dist为分割角点和图像边界最少像素数

#寻找高于阈值的候选点
corner_threshold = harrisim.max() * threshold
harrisim_t = (harrisim &gt; corner_threshold) * 1
#得到候选点的坐标
coords =array(harrisim_t.nonzero()).T
#计算候选点响应值
candidate_values = [harrisim[c[0],c[1]] for c in coords]
#对候选点按照响应值进行排序
index = argsort(candidate_values)
#将可行点的位置保存到数组
allowed_locations = zeros(harrisim.shape)
allowed_locations[min_dist:-min_dist,min_dist:-min_dist]=1
#按照min_distance原则选择最佳Harris点
filtered_coords = []
for i in index:
if allowed_locations[coords[i,0],coords[i,1]] == 1:
filtered_coords.append(coords[i])
allowed_locations[(coords[i,0]-min_dist):(coords[i,0]+min_dist),(coords[i,1]-min_dist):(coords[i,1]+min_dist)] = 0
return filtered_coords

def get_descriptors(image,filtered_coords,wid):
#对返回的坐标点，获取2*wid+1个像素的值，即获取harris描述
desc=[]
for coords in filtered_coords:
patch = image[coords[0]-wid:coords[0]+wid+1,coords[1]-wid:coords[1]+wid+1].flatten()
desc.append(patch)
return desc

def match(desc1,desc2,threshold=0.5):
#特征点匹配，使第一幅图中的角点描述子利用归一化相关选取它在第二幅图像的匹配角点
n = len(desc1[0])
#每对点的距离
d = -ones((len(desc1),len(desc2)))
for i in range(len(desc1)):
for j in range(len(desc2)):
d1 = (desc1[i]-mean(desc1[i])) / std(desc1[i])
d2 = (desc2[j]-mean(desc2[j])) / std(desc2[j])
ncc_value = sum(d1 * d2) / (n-1)
if ncc_value &gt;threshold:
d[i,j] = ncc_value
ndx = argsort(-d)
matchscores = ndx[:,0]

return matchscores

def match_twosided(desc1,desc2,threshold=0.5):
#两边对称版本的match
matches_12 = match(desc1,desc2,threshold)
matches_21 = match(desc2,desc1,threshold)

ndx_12 = where(matches_12 &gt; 0)[0]
#去除非对称的匹配
for n in ndx_12:
if matches_21[matches_12[n]]!=n:
matches_12[n] = -1
return matches_12

def appendimages(im1,im2):
#拼接两幅图像
rows1 = im1.shape[0]
rows2 = im2.shape[0]
if rows1 &lt; rows2:
im1 = concatenate((im1,zeros((rows2-rows1,im1.shape[1]))),axis=0)
elif rows1 &gt; rows2:
im2 = concatenate((im2,zeros((rows1-rows2,im2.shape[1]))),axis=0)

return concatenate((im1,im2),axis=1)

def plot_matches(im01,im02,locs1,locs2,matchscores):
#显示一副有连接线的匹配图像
im3 = appendimages(im01,im02)
im4 = vstack((im3,im3))
imshow(im4)

cols1 = im1.shape[1]
rows1 = im1.shape[0]
for i,m in enumerate(matchscores):
if m&gt;0:
plot([locs1[i][1],locs2[m][1]+cols1],[locs1[i][0],locs2[m][0]],'c')
new_coords =[]
for j in filtered_coords1:
new_coords.append ([j[0] + rows1, j[1]])
for i in filtered_coords2:
new_coords.append ([i[0] + rows1, i[1] + cols1])
plot([p[1] for p in new_coords],[p[0] for p in new_coords],'*')
axis('off')

min_dist = 7
wid = 6
threshold=0.1
im01=array(Image.open('1.JPG'))
im02=array(Image.open('2.JPG'))
im1 = array(Image.open('1.JPG').convert('L'))
im2 = array(Image.open('2.JPG').convert('L'))
harrisim = compute_harris_response(im1,5)
filtered_coords1 = get_harris_points(harrisim,min_dist,threshold)
print 'Harris Points in 1.JPG:'+bytes(len(filtered_coords1))
d1 = get_descriptors(im1,filtered_coords1,wid)

harrisim = compute_harris_response(im2,5)
filtered_coords2 = get_harris_points(harrisim,min_dist,threshold)
print 'Harris Points in 2.JPG:'+bytes(len(filtered_coords2))
d2 = get_descriptors(im2,filtered_coords2,wid)

print 'start matching'
matches = match_twosided(d1,d2)
print 'Matched Points in 1.JPG and 2.JPG:'+bytes(len(matches))
figure()
gray()
plot_matches(im01,im02,filtered_coords1,filtered_coords2,matches)
show()

其中输入图像在python程序的同目录，为两幅近似的图像。其结果一举不同的min_dist和threshold而改变。

 

*.py文件打包成.exe可执行文件

这里使用的是PyInstaller将py文件打包。实际效果非常方便，会自动搜寻需要的库并合成。可到其官网下载最新版2.1

基本语法是

python pyinstaller.py [opts] yourprogram.py

其中opts是可选项，可加入的参数为：

-F, –onefile 打包成一个exe文件。
-D, –onedir 创建一个目录，包含exe文件，但会依赖很多文件（默认选项）。
-c, –console, –nowindowed 使用控制台，无界面(默认)
-w, –windowed, –noconsole 使用窗口，无控制台

BUG

这里遇到了恼人的无可药救的无与伦比的bug。其中之一是

no module named _ufuncs

阅遍无数网页终于在这里发现了解决方案，需要在PyInstall文件夹的hooks文件夹中添加一个寻找 _ufuncs的py文件。在这里 ，命名为hook-scipy.special._ufuncs.py

#-----------------------------------------------------------------------------
# Copyright (c) 2013, PyInstaller Development Team.
#
# Distributed under the terms of the GNU General Public License with exception
# for distributing bootloader.
#
# The full license is in the file COPYING.txt, distributed with this software.
#-----------------------------------------------------------------------------

# Module scipy.io._ufunc on some other C/C++ extensions.
# The hidden import is necessary for SciPy 0.13+.
# Thanks to dyadkin, see issue #826.
hiddenimports = ['scipy.special._ufuncs_cxx']

然后又发现另一个bug，这回是

no module named integrate

阅遍无数网页，依然没有结果。。偶然的在需要编译的py文件中加入了一句
from scipy.integrate import *
咦居然成功了。。。好吧。结果出来就和在python shell中运行的一样了。可以打包成一整个exe文件，也可以是一个文件夹，包含其他类库的。

1.在需要添加控制台调试的cpp页面加上#include “conio.h”;

2.在启动mfc窗体的页面加入AllocConsole();

3.在需要输出的地方输入 cprintf() ,其中是char类型。若是vs2005之后，应改成_cprintf();

4.若需要关闭控制台窗口，使用 FreeConsole();

最近在Stanford的网络课程学习了机器学习的课程，Andre Ng讲的灰常不错啊。每种算法对应的实例挺多的，推导也很详细，它基本用matlab实现。就是概率统计数理统计矩阵论方面的知识最近得补一补了，直接应用在编程语言编写某些函数也是挺头疼的，不错还是略有收获。总共20节，听完5节，做个小结。

[L1 Introduction]
凸优化理论 隐式马尔科夫模型 O natation 学习型算法

1)Supervised Learning
回归问题 Regression 分类问题(x|y)(肿瘤大小|癌症良恶) 学习给定了标准答案的样本->分析新样本的可能性 支持向量机Support Vector Machine
2)Learning Theory
3)Unsupervised Learning
挖掘 聚类分析->图像分析和处理的应用 像素处理 ICA Algorithm 鸡尾酒问题（不同声源声音分离）
4)Reinforcement Learning
决策分析

 

马可夫过程

在概率论及统计学中，马可夫过程（英语：Markov process）是一个具备了马可夫性质的随机过程。马可夫过程是不具备记忆特质的（memorylessness）。换言之，马可夫过程的条件概率仅仅与系统的当前状态相关，而与它的过去历史或未来状态，都是独立、不相关的。具备离散状态的马可夫过程，通常被称为马可夫链。马可夫链通常使用离散的时间集合定义，又称离散时间马可夫链。具有马尔可夫性质的过程通常称之为马尔可夫过程。

	可数或有限的状态空间	连续或一般的状态空间
离散时间	在可数且有限状态空间下的马可夫链	Harris chain (在一般状态空间下的马可夫链)
连续时间	Continuous-time Markov process	任何具备马可夫性质的连续随机过程，例如维纳过程

##

具有马尔可夫表示的非马尔可夫过程的例子，例如有移动平均时间序列。最有名的马尔可夫过程为马尔可夫链，但不少其他的过程，包括布朗运动也是马尔可夫过程。

 

隐马尔可夫模型

 

隐马尔可夫模型（Hidden Markov Model，HMM）是统计模型，它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析，例如模式识别。在正常的马尔可夫模型中，状态对于观察者来说是直接可见的。这样状态的转换概率便是全部的参数。而在隐马尔可夫模型中,状态并不是直接可见的，但受状态影响的某些变量则是可见的。每一个状态在可能输出的符号上都有一概率分布。因此输出符号的序列能够透露出状态序列的一些信息。

隐马尔可夫模型最初是在20世纪60年代后半期Leonard E. Baum和其它一些作者在一系列的统计学论文中描述的。HMM最初的应用之一是开始于20世纪70年代中期的语音识别。 在1980年代后半期，HMM开始应用到生物序列尤其是DNA的分析中。此后，在生物信息学领域HMM逐渐成为一项不可或缺的技术。

HMM有三个典型(canonical)问题:
已知模型参数，计算某一特定输出序列的概率.通常使用forward算法解决.
已知模型参数，寻找最可能的能产生某一特定输出序列的隐含状态的序列.通常使用Viterbi算法解决.
已知输出序列，寻找最可能的状态转移以及输出概率.通常使用Baum-Welch算法以及Reversed Viterbi算法解决.

 

凸优化

 

凸优化，或叫做凸最优化，凸最小化，是数学最优化的一个子领域，研究定义于凸集中的凸函数最小化的问题。凸优化在某种意义上说较一般情形的数学最优化问题要简单，譬如在凸优化中局部最优值必定是全局最优值。凸函数的凸性使得凸分析中的有力工具在最优化问题中得以应用，如次导数等。
凸优化应用于很多学科领域，诸如自动控制系统，信号处理，通讯和网络，电子电路设计，数据分析和建模，统计学(最优化设计），以及金融。在近来运算能力提高和最优化理论发展的背景下，一般的凸优化已经接近简单的线性规划一样直捷易行。许多最优化问题都可以转化成凸优化（凸最小化）问题，例如求凹函数f最大值的问题就等同于求凸函数 -f最小值的问题。

凸优化（凸最小化）问题可以用以下几种方法求解：
捆集法
次梯度法
内点法

[L2]Linear Regression线性回归 Gradient descent梯度下降 Normal equations正规化方程组（都需要矩阵变换知识）

{(x(i), y(i)); i =1, . . . , m}称作包含m个训练样本的训练集合

h是假设的模型，可以带有一定先验知识，也可以是推测类型。学习算法通过学习训练集合的样本，得到h假设中的一定参数，在新的样本中进行预测和他推理。若目标变量y是连续的，则这样的学习问题可归为回归问题；若目标变量y是离散的，例如可在{0,1}中取值的垃圾邮件归类、癌症可能性判定问题，则可归为分类问题。

假设h假设是线性的，则假设就是各个参数线性的代数和。其中θ和x均是向量。x中各向量分量是各自变因素的取值，θ是各个自变量分量的系数或权重。则机器学习算法的目的就是求这个假设函数h(x)与真实值y的最小值。评估标准J(θ)以各样本和预测值的差的平方的二分之一为准。（二分之一纯粹是为了后期的运算）

1. LMS（ Least mean square） 算法

即最小均方算法。算法实质是自适应的纠错学习，在学习中纠正参数θ的取值，直到收敛。其中，运用的最多的是梯度下降算法（Gradient Descent）

算法步骤为：

a)选取一个初始参数向量，可令其为0向量

b)重复查找各方向梯度，沿着梯度下降最快的方向搜索

c)直到四周均比局部梯度大的局部最优点

算法的数学描述为（该式为原始式，即梯度下降的数学定义）：

：=与计算机编程中的赋值语句等同。α称作学习比率。则上式中J(θ)对θ求导的数学推导式为：

这里更新最上式，对于单个训练样本

对所有训练样本，沿着梯度方向不断计算直到收敛

该方法中，每一次梯度的计算都用到了每个训练样本，这种梯度下降的方法称为 批梯度下降。由于这里的最优化问题只有一个全局，因此这里的局部梯度最优点即是全局的梯度最优点。此外还可以采取随机梯度下降，每次梯度的计算选取随机的样本点，这样收敛的速度更快，但可能永远不会收敛到最优点，但会集中在最优点附近。因而在训练样本较大时可以采用随机梯度下降。这是随机梯度下降算法的数学表达：这是利用批梯度下降算法计算的梯度直到收敛，可以注意到每一次步长是不一样的，步长可在学习中不断调节，越接近最优点步长越短。

2.正规化方程

梯度下降是一种求取价值函数J(θ)的方法，正规化方程是另一种方案。首先提到的是几个必要的矩阵知识：

f与向量A的映射关系中，对f进行求导的定义：

关于迹的一些定理：

迹的乘法交换：

迹和转置的迹；迹的加法结合；迹的数乘

迹与倒数相关：

上式中，B是n_m矩阵，f的定义是依赖m_n矩阵的函数f（A）的值等于AB的迹。其中f（A）中的A的含义是A矩阵的每一个矩阵分量。

将J(θ)写成矩阵形式，给定的训练集合定义成矩阵X（m*n）m是训练样本个数，n是每个训练样本的自变量分量。

则已知的结果也可以用矩阵表示，或者说是向量表示

假设h和y的向量差为

J(θ)则可以表示为：

可以看到，h-y利用了向量内乘的方式，即向量乘以向量的转置，得到的实际上是个一维矩阵即一个数。为了找到J(θ)的最小值，可利用矩阵的求导，并参考上式中迹与倒数相关第三条：

第三步骤中，利用到实数的迹也是它本身，第四步中用到了迹和迹的转置，第五步中的方法是利用迹与倒数相关第三条，将A的转置设为θ，B=B的转置=X的转置*X C=单位阵，带入公式即可。令上式为零，则求出导数为零时θ的取值。得到的方程称为正规化方程：

梯度下降

梯度下降法，基于这样的观察：如果实值函数 F(x)在点 (a,f(a)) 处可微且有定义，那么函数 F(x)在 a点沿着梯度相反的方向 -▽ F(a) 下降最快。

因而，如果,对于 为一个够小数值时成立，那么 。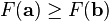

考虑到这一点，我们可以从函数 的局部极小值的初始估计 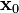出发，并考虑如下序列 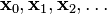使得

因此可得到如果顺利的话序列 收敛到期望的极值。注意每次迭代_步长_ 可以改变。假设 定义在平面上，并且函数图像是一个碗型。蓝色的曲线是等高线，即函数 为常数的集合构成的曲线。红色的箭头指向该点梯度的反方向。（一点处的梯度方向与通过该点的等高线的垂线。沿着梯度_下降_方向，将最终到达碗底，即函数 值最小的点。

 

最近有使用到CloudCompare，是一个开源的可视化显示三维点云的程序。

• 项目首页
• Github
• wiki

CloudCompare功能较为丰富，可以处理3d点云数据，可以比较两幅3d点云图像（例如激光扫描获取的图像）亦或者比较一副点云图像和一副三角网。它基于独特的八叉树结构使得性能极大的提升，一般可同时处理超过一千万点云数据，最高可在2Gb的内存下处理1.2亿个点云数据。该软件有可执行文件exe,也可以在linux、mac、windows中编译后使用最新的功能。项目首页有exe、7z版本的完整版、7z简化版的CCviewer，本次编译使用Windows8.1 64bit系统、MS Visual Studio2013 64bit，使用项目的github代码在Cmake下编译。

编译环境：

1. Qt5.4 Qt中需要下载一个Qt 5.4.1 for Windows 64-bit (VS 2013, OpenGL, 711 MB) (info)来安装Qt的环境，还需要下载一个Visual Studio Add-in 1.2.4 for Qt5 (156 MB) (info)来在VS中进行可视化编辑。
2. Cmake Cmake是一个根据不同系统和配置进行编译的工具，在windows、linux和mac都可以使用。windows下64位系统可以正常安装32位版本。
3. 利用svn checkoutgithub中的最新项目。这里地址为G:\CCViewer\trunk

参考这里开始编译：

1. 在编译好的文件G:/build中打开sln，先重新生成解决方案。打不开。参考这里，先右键在项目属性中选择debug（编译）将命令那一栏改成debug文件夹下的CloudCompare.exe文件。
2. 最后找不到各种*.dll，在qt的安装文件夹中找到，放到项目的debug文件夹中，若是qcc是完整版，ccviewer是浏览器简版，均是放在相应的debug文件夹下。

这样就完成了编译，若需要在vs中编辑qt的窗口，需要在qt的菜单栏选项中指定qt版本和相应的地址，参考这里，点击Add，写入 版本号5.4.1和地址E:\Qt\Qt5.4.1\msvc2013_64_opengl,这样双击项目中的ui就可以在qt的可视化编辑器中编写qt窗口。。里面的函数封装好复杂，，窝先匿去研究一会儿了。

春节档简直是近5年最烂的 国产保护加上喜庆保温 导致所谓最强的影片「狼图腾」也差强人意 主题和细节都没能相当程度上还原原著 更别提钟馗伏魔 澳门风云二这样稀烂的影片了

 

「少年时代」

伙伴 陪伴 和自己的成长 这就是最朴素 最大众的少年时代 最写实的美国家庭 姐弟 新朋友 新家庭 新恋情 新的开始 18岁。执着的剧组和执着的男主家庭 用12年撑起了一个自己的纪录片 若要说一些遗憾 便是 少了些许波澜和累点罢 或许生活都这样⭐⭐⭐⭐

 

「有一个地方只有我们知道」

文艺老徐 好男人帅哥 穿越时空的爱恋 等一个人 王朔的剧本很婉转 梦一样让人回味 布拉格 老房子 水晶围脖 一封信 老车票 一尊永远在那儿的雕塑 对的人，你是不会失去的。。似青春又纷纷错过 似回忆总记不起 双线结构以老少相遇作为交点 些许落入俗套 吴亦凡王丽坤一类的偶像演员让平静暖心的剧情变得热火朝天 不时耳语尖叫拍凳跺腿 加上布拉格东欧浪漫文艺的风景 让小说剧情电影实实在在成了偶像剧 也罢情人节唯一的爱情剧吧 ⭐⭐⭐⭐

 

「狼图腾」

毕竟小说的影响力超过了电影不止一两个数量级，电影也精选了小说的几个重要的节点和精彩桥段 暴风雪夜与狼的决斗 与小狼的故事 刨狼的猎物 构成了电影的主要情节 草原上的故事也相对圆满的完成了人与自然取舍和相处的主旨传递 也成为了春节档独特突出的异类主题 且不谈拍摄草原的艰辛和狼形态的捕捉 单是时间跨度就足以见得设置组的用心 美中不足便是冯的演技还是略微僵硬 ⭐⭐⭐⭐

 

「逃离德黑兰」

剧情较为无趣 逃离的拍摄实在有些险峻而超离实际 宣扬大义大勇的拯救公民 以及拯救敌意世界意识形态暴力黑的典型 与刺杀金正恩等都有类似的资本主义潮吹的感慨 既然是得到了西方各大电影节认可的电影 唯一印象深刻的是躲在加国大使馆的美帝人员的紧张和凌乱变现的异常出彩 相比是比较中庸而符合G点的⭐⭐⭐

 

「天将雄师」

各种混搭各种奇葩 中西合璧的成龙大哥和 乱入的朱孝天崔始源 还有捧哏和逗哏的筷子兄弟 就这样奇葩的馅料居然还捏成了不错的饺子 大汉天国终于和古罗马骑兵来了一次穿越搏击和惺惺相惜 龙哥的光环强的无限续命 主角以开头就注定了死掉的命运 好惨的是死的还这么简单 但作为毫无特效的古装漠片能紧扣剧情一气呵成也不容易 给春节档一个惊喜⭐⭐⭐⭐

 

「澳门风云2」

不多谈 粤式无厘头笑点 无3d的3d片 春节呵呵不起来的嘻嘻档 烂 ⭐⭐

「一路惊喜」

虽然格调挺俗的 虽然演员挺作的 虽然情节挺狗血的 但是我居然感到了一丝暖意 挺好 ⭐⭐⭐⭐

 

「模仿游戏」

看点除了卷福的超群演技外 似乎并没什么深刻人心的 没有残酷的谍战 没有缜密的逻辑推理和演绎 没有繁复的破解技巧和战争胜利的重要性 只有时间段的跳跃 被基佬利用的爱情 和实验室（算是在做实验吧 和一大群基佬们的斗智斗勇和最后争夺经费和战略隐瞒的剧情冲突 但这就正是电影节电影的思路 對基佬對打擊 對戰爭勝利至高重要性對年代 對人性大義對褒獎 都是獲得普遍認可的重要原因 ⭐⭐⭐⭐