近期忙着撸工作。边学边总结。
16-11-03
蛇精网络中,激活函数一般选择sigmod或者双曲正切函数。即
$$
f(x)=\frac{1}{1+e^{-x}}
f’(x)=f(x)(1-f(x))
$$
或
$$
f(x)=tanh(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}
f’(x)=1-(f(x))^{2}
$$
一个神经元的主要过程有:
- 综合输入,根据Wx+b计算每个输入的滤波结果(可理解为线性变换),其中W是维度和输入相当的矩阵,b是截距,一些时候可以写入W里,同时增加一个齐次坐标1。
- 计算结果的sum
- 将结果作为输入载入激活函数,判断激活度,以偏置函数判断是否激活该节点。
16-10-08
CDN-dns服务器的CNAME如果指向dns智能负载均衡服务器,则通过CDN指派最快的的节点(一般根据用户IP)解析域名获取IP地址,并把缓存服务器没有超过TTL的内容直接传送给用户,包括静态页面、图片等。极大的节省了带宽和网络延时。每个节点都包含高速缓存服务器和负载均衡服务器,主要的内容有
约瑟夫环-通项公式为F(1)=0;F(i)=F(i+m)%k,循环从2-N。其中i为有i个人参与游戏,F(i)为i个人参与游戏最后一个人的ID(0开始的ID)
mysql主从备份-也叫双热备份。主要执行的是可中断的备份程序,在配置文件ini或者cnf中设置主从关系(密码,用户名,host,ID),然后grant duplication 设置slave的权限。然后使用逻辑备份的mysqldump进行备份。
索引的设置:在经常查询、连接(主要是外检)、排序、group by、范围查询的列上进行可以显著加快查询效率;不应在修改性能远大于检索性能、数值范围很少、查询较少、数据类型为textimagebit等的增加索引。主要有三种索引类型:唯一索引(不允许任意两行相同)、主键(唯一表示数据行的某列)索引、聚集索引(物理顺序与逻辑顺序相同)。
范式-第一范式 每一列不可以有多个值;第二范式 每个实例或行必须被唯一地区分。(一般用primary key);第三范式 不依赖其他非主属性
数据库优化-
1.SQL(避免使用!= <>操作符,否则将放弃索引进行全盘搜索;避免null值判断、exists替代in,多用where替代having)
16-09-17
2.索引 如上
3.范式优化 消除冗余 适当增加冗余较少jion 表分区。
4.水平(解决单表数据增量)、垂直(解决IO 按照增量拆分)拆分表(适应增长)
……我以为 我快挂了呢。保持稳定,保持自信。去了趟深圳,投错了门。笔试了N家,家家挂。阿里、腾讯、猿题库、美团、网易互联网、搜狐畅游、爱奇艺、携程……AA啊等着吧。百度-卒;当当=卒;长光-卒;大疆-卒;招行-?
关于熵和最大熵和其他
最近学习到了有关决策树的部分。分裂特征的时候ID3选择的就是熵减少最多的那个特征来进行。所有熵在信息论、物理、系统概论里面好多地方都用到了。
- 熵的两种表述是不稳定性和信息量,越不稳定信息量也越多,反之亦然。物理系统里可以解释为混乱程度,体系能量程度。
- 最大熵理论解释为在已知情况下,不知道的部分最有可能是趋于其最混乱信息量最大最平均的情况。即最大熵是在未知信息的最一般最朴实理解,解释该情况的一个最普遍的实例就是,对一个未知的筛子每个面掷出的概率都是1/6.最大熵保留尽可能大的不确定性而作出最佳的尽量无偏差的决定。
- 熵=信息熵,联合熵=独立分布事件的所有信息量(可能有信息量重叠),信息量重叠的部分即为互信息,条件熵是在已知某(些)事件发生时,另一件事件的所剩信息量,很显然,条件熵+互信息=信息熵。
最基本的一条公式即为信息熵的公式。然鹅,大多数推公式都给出其表达,再给出其性质。恰恰相反,本质上该公式的表达则是从其应具有的性质上得出。由于越未知信息越多熵越大,信息熵具有的性质为:
- 光滑连续的
- 信息应该是能叠加的,相加应大于等于部分
- 当两个变量是独立分布的时候,F(x)F(y)理应等于F(x)+F(y).->显然,这里能够具有该性质的应该是对数函数
- 信息越大熵越大
取二项分布时的状态,可以得到$$-\sum_{i=0}^{n}p_{i}(x)lg p_{i}(x)$$.底可以取任何数。
一个通俗的例子解释就是->
- pi为该情况的概率,例如数学之美丽提到的,世界杯一个队夺冠的概率是1/32
- 1/pi为独立出现一次这样情况的需要的次数.例如,在不知道情况的情况下,大家实力一样,则1个队夺冠一次需要的次数参加世界杯的次数为32
- $$lg(\frac{1}{p_{i}(x)})$$为系统确认该状况,需要几次。底为2说明系统每次能够区分2个度的情况,例如天平称重量,例如二叉查找树二分查找。猜测世界杯冠军时,当取2为底,表示每次能确认一半的信息,即二分询问lg(pi)=5;若取32为底,则表明每次确认1/32的信息,即挨个球队问问。lg(pi)=1.
- $$p_{i}(x)lg p_{i}(x)$$由于高概率事件常出现,低概率事件不经常出现,其概率与系统表达该情况次数相乘,即为表达该事件所需要的概率次数。
- 取所有情况的和,即为系统复现所有概率可能需要的平均次数(也可能为长度、时间等)
另一个客观的例子即字符串的概率和二进制的表达。某些二进制字符出现的概率为p(xi),则样本中需要1/p(xi)次才会出现一个这样的字符,二进制表示需要lg(1/p(xi))位,则每表达一个字符串给与其权重为其出现的概率再求和,即平均每个样本所需要系统复现(表达、分辨)所需要的平均次数(平均信息量)。
系统每次表达两种情况,记做·bit;系统每次复现e种情况,记做ln。然鹅,我们并不关注系统每次能解决多少情况,我们关注的是相同的系统下,不同的时间的概率分布有多少信息量。一般呢,就取lg
16-08-31
Logistic回归是广义上的线性回归(将y变为lny)。它使用了一个单增可微函数,因而损失函数(预计值与实际值以某种函数表达的差异)接近。实际上它们都是指数分布族的函数。
关于布冯投针试验,3个简易的理解方式(线宽为L 针长为a):
- 扔圈圈法
直径为线宽(长度为时πL)的圆扔过去,必有两个点,扔n次必有2n个交点。根据机会均等原则,折成直线的情况扔过去,可能会有0,1,2,3,4个交点,但扔n次也必有2n个点。当针长为a时,显而易见的是a与交点个数m成正比,即m=αa.令a=πL,m=2n,∴α=2n/(πL),又相交概率P=n/m,所以联立
$$ \pi =\frac{2a}{LP} $$ - 概率密度函数法
另一种方式根据概率,针中点距离最近的一条线的距离x和与线成的角度Θ服从独立分布,其中
x∈[0,L/2],服从均匀分布,其概率密度函数为2/L
Θ∈[0,π/2],服从均匀分布,其概率密度函数为2/π
由于x,Θ是相互独立的,所以两者结合的概率为两者概率密度函数的积:4/πL。
当满足相交的条件时,x≤a/2*sin(Θ)。凡是一切满足该情况的积分起来就好了。
$$P=\int_{0}^{\frac{\pi }{2}}\int_{0}^{\frac{a}{2}sin(\theta)}\frac{4}{\pi L}dxd\theta =\frac{2a}{\pi L}$$亦可得到上解法。
16-08-29
py的机器学习包调用的好的好简单啊。。数据清洗和筛选都很舒服。。
关于Java集合框架(JCF),主要的接口和类有: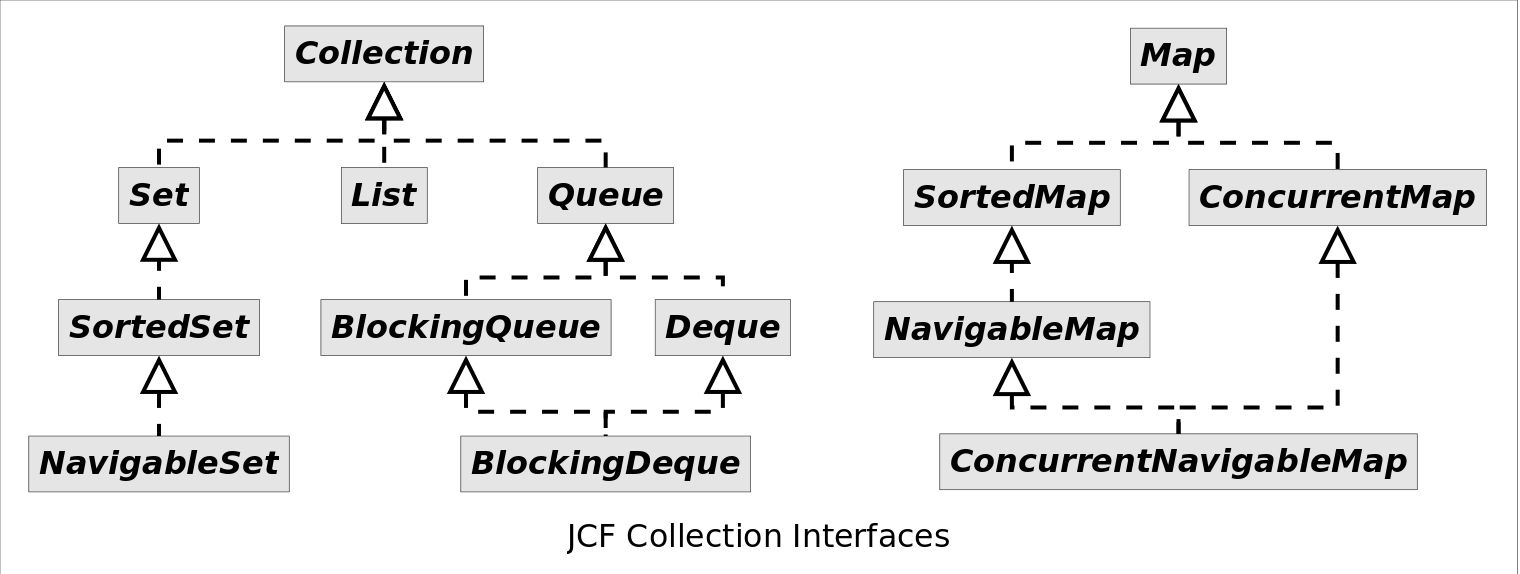
List下面都有提到,现在主要来讨论Set和Queue。值得一提的是,Set其实是一种特殊的Map。将键和值都赋为相同的值,Set为Map的一种适配器模式,即只实现了想实现的功能,其他Map的功能我不要。同时,由于在JDK1.6以后,Deque实现了双向链表的功能,也封装了顶部加入和弹出、底部加入和弹出的功能,实际完成了Stack的基本操作,所以Stack基本被Deque取代了。可以将Deque看做实现了基本所有优先队列功能的接口,其唯一实现类是LinkedList(它继承自AbstractList,因为也带有List基本的功能,好屌啊).
这个很重要
下图为集合框架的实现方式。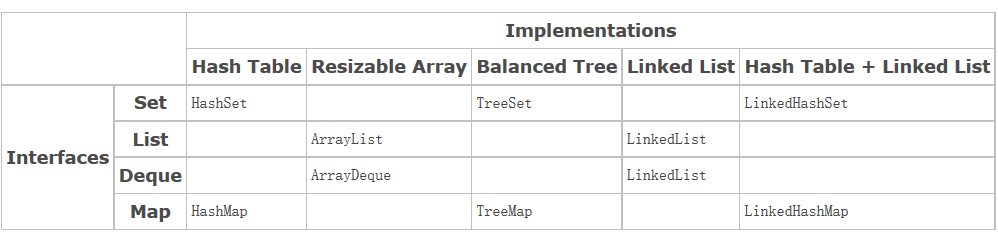
可以看到,LinkedList几乎即实现了双链表又实现了List集合的功能;而基于红黑树的TreeMap和TreeSet能在O(lg(n))时间内完成数据的插入、删除、查找等基本操作。而链表和数组不同方式实现了的List则对于插入和删除有显而易见不同的时间复杂度。LinkedHash两者并存也是神奇的存在,一个Map里,在哈希表的slot里面插入同一位置的使用链表存放,并把链表尾端链到下一个有值的槽的键值上。。虽然很好用,但是,大量的数据需要开很大的空间来存放指针。
集合框架都能使用.hasNext函数来使用迭代器进行遍历,当然,foreach大法也很好。
16-08-28
近日复习了机器学习线性回归和Logistic回归。前者只需记住j(Θ)的推导和最终结论$$\theta =(X^{T}X)^{-1}X^{T}Y$$或者$$\theta =(X^{T}X+\lambda I)^{-1}X^{T}Y$$即可;为了排除求逆的复杂度则进行梯度下降也是极好。
- Batch(批量梯度下降)
$$ \theta_{j} += \alpha \sum^m_{i=1}(y^i-h_\theta(x^{(i)}))x^{(i)}_j$$
其中α是步长(学习因子),h为Θ相关的预测,xy均已知,该方法每步需迭代所有数据 - stachastic(随机梯度下降)
$$ \theta_j += \alpha (y^i-h_\theta(x^{(i)}))x^{(i)}_j$$
同上类似 但每步只加入一个数据进行梯度计算迭代。 - mini batch(结合上俩式结合一小部分的数据进行迭代而非全部也不是一个)
- 回归不适用于分类,尤其是多分类。原理回归曲线的点会严重影响回归函数。
- 局部加权回归是在求解梯度时在求和部分加入一个ω函数,使得残杀服从某种分布,一般选择ω为高斯核函数。
- J(Θ)采用的是似然函数求取极值的方式来计算参数;回归时很可能需要先验知识对数据加入某一特征的二次、三次作为新的特征来拟合回归函数。
16-08-25
复习leetcode的一些基本题。两个排序数组取中值的,这个真心想了好久。虽知道是分支,但就是解决不好头尾和递推条件。还有很经典的子数组max和,子数组max积,股票买卖那几个动归的问题。单独拿那个取中值的说一下。
这个算法最直接的当阿然是O(n)把排序数组重合。与快拍里面的一小节类似。但是要更快,就需要更好的思维过程了。
想到分治必然是划分小区间,然而已经有两段了如何划分更 .0小的区间,一划就成4个了。然而转念一想,取中值,必然是两组里面分别小于中值的和两组里面分别大于中值的共四组。设A B倆数组,长度分别是m,n.约定划分在i∈[0,m-1],j∈[0,n-1]。这样,AB分为了左右两组,
| Left | Right |
|---|---|
| A[0]~A[i] | A[i+1]~B[m-1] |
| B[0]~B[j] | B[j+1]~B[n-1] |
当且仅当以下条件满足时,找到了合适的i和j。
- A[i]<B[j+1]且B[j]<A[i+1] (即保证严格左堆小于又堆)
16-08-24
关于高并发 synchronized可以针对静态函数 实例方法和类对象进行阻塞。当访问到里临界区资源时,不但不能写入,同时亦不能读取,防止读取到副本而做出超出预计的运算。HashMap和ArrayList在多线程时一定不能用。
针对synchronized很方便的加锁方式,重入锁可以很好的完全替代它。它的主要作用有在中断时给予响应,对某锁申请限制时间的等待,给与申请锁的线程公平的获得机会(防止饥饿产生)。其主要的方法有:
- lock()获得锁 如果已被占用则等待。
- lockInterruptibly()获得锁,但有响应则优先
- tryLock()尝试获得锁,获得失败直接返回false,获得成功则返回true
- tryLock(long time,TimeUnit unit)一个参数表示长度,一个参数表示单位。限定时间内尝试获得锁。
- unLock()释放锁。
而使用condition来配合完成wait和notify操作。
16-08-22
关于ArrayList与Vector
同步性及线程安全不同、自增方式不同;底层均基于数组(Object[])实现,可随机访问,查询增删效率相同。
List
LinkedList通过双链表维护,因而可以轻易的转换为栈和队列(Stack Queue Deque)等优先队列的结构。
要得到一个同步的LinkedList可以使用同步封装器实现,从Collections.synchronizedList(List)得到。但Vector就不需要进行额外的调用,尤其是在访问和更新。
LinkedList定义了专门用于表头和表尾操作的方法。Vector提供了indexOf(obj,start)接口,arrayList没有这个。
List和Map中,只有Vector和HashTable能维护高效的同步
List的继承链大致为
+--java.util.Collection[I](集合框架接口)
+--java.util.List[I](存放一类元素 可重复 有序 以下三者均继承自抽象类AbstractList,由其实现List接口。)
+--java.util.ArrayList[C]
+--java.util.LinkedList[C]
+--java.util.Vector[C]
所有的类要么继承自List要么继承自Set,不能直接实现Collection。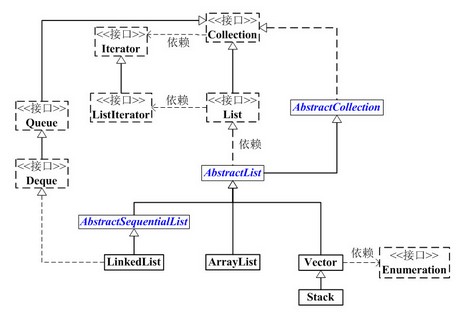
AbstractList是一个抽象类,继承自AbstractCollection,AbstractList实现了除size()和get(int location)之外的函数。LinkedList与正常基于数组的不同,其通过AbstractSequentialList这一抽象类继承了AbstractList并额外添加了对链表的各项操作,又实现了Deque接口而完成了双向链表的功能。可以看到,Queue和Deque的唯一实现类都是LinkedList.Stack该类继承自Vector,完成了先进后出的操作。
关于线程安全
线程安全的类 ,指的是类内共享的全局变量的访问必须保证是不受多线程形式影响的。
多线程保持原子性、可见性、有序性(涉及指令重排)
16-08-21
复习了小顶堆 大顶堆的插入。以树为逻辑以数组为存储的结构。初始化第一个位置置为null或者0.插入在末尾进行heapUp,删除替换末尾进行heapDown,排序也是进行heapDown的操作。
16-08-20
TreeMap是基于红黑树的SortedMap的实现。SortedMap是基于键的大小自动运行比较器的Map集合框架,正规的实现该接口必须包括:
- 不含餐的构造函数 插入时按照键自然顺序排序
- 实现一个comparatot的构造函数 按照比较器给定的顺序排序。该比较器应定义良好。
- 带Map的构造函数 创建参数相同的有序映射 按照自然顺序排序
- 带有序映射类型的构造函数,使其顺序、比较方式、键值映射关系与给定有序映射类型相同
其修改不是同步的,不是线程安全的。所以尽量在创建时完成这一操作,或使用Collections集合的同步方法,如:
Map m = Collections.synchronizedMap(new TreeMap(...));
其他:key不可以为空,value可为空;相同值的插入会覆盖前面的。
16-08-20
心疼李宗伟
复习了树的前驱后继的求法。求前有左求后有右都好求,关键的是相反的话,需要记录最接近的拐点,同时记录父母亲(如果是向的树),这样可以避免中序遍历的O(N)时间复杂度而变成O(lg(N))的二分查找复杂度。
16-08-18
复习了非递归树的遍历 主要是栈的应用。利用单队列 双队列实现层次遍历。树的旋转还是容易变化,删除操作里的三种情况也要记住。删除二儿子节点找到前驱或者后继(右子树最左 左子树最右)并替换之,并按照一儿子或者0儿子的删除将该节点删除。
16-08-17
tire树几个特征:适用单词(短语)模糊推荐 N叉树-多基于单词分叉-每个节点独设标记位记录是否为单词节点 一些方案中记录共用该节点单词数(非到叶子路径数)使得查询时间复杂度O(lg(kN)).k为当前查询字符长度 N为最多分支数。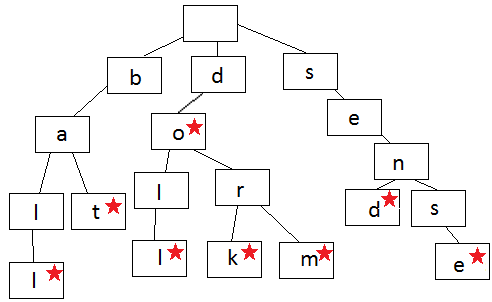
尝试一下 有道的网页笔试 其中一道题是分两摞的洗牌问题。从上到下1、2……N标号的纸牌,各取一半,左下取一张,右下取一张,左下取第二张,右下取第二张……以此类推,和正常洗牌类似,求k次洗牌后的顺序。牌堆编号给出。例如1,2,3,4,5,6洗一次后变为4,1,5,2,6,3.额。。。尝试了暴力求解 但是应该能有什么规律似的。尝试给每张牌记录是否存在的记号,还是略微痛苦。
接近刷完了算法导论的课程,更多的接近于概率论的算法证明课。收获的很扎实,但是还是书看的快,权当是复习算法的内涵和合理性部分了。
