http://ju.outofmemory.cn/entry/106397 【坑妹填完】
最近各种乱整。。文章妹时间管光顾着折腾手头派下来的事情了。再加上每天固定的复习提高一下。小论文完全没有头绪。
最近get到的实用方法还是很多阿。
DBScan(Density-Based Spatial Clustering of Applications with Noise)基于密度的含噪空间聚类
最大特点是:多维、任何形状聚类、聚类数任意、噪声可控、对输入不敏感;缺点很明显,需要提前知道2个参数(一般实验多了,根据经验对同一类型聚类可以不用改。),时间复杂度和空间复杂度都很大,需要计算点两两之间距离[这里需要优化,否则算法超出一般忍受时间] 不对密度变化做出选择。
输入参数2个,单一点半径范围R及其最小包含的点数N。算法本质是遍历所有点并计算邻域内的点数并拓展该类(以R范围内是否达到N来判断)。被分类的点将会标记并不再被检测到。因此耗时表现在邻域查找和拓展聚类上。但解算效果相当良好。
算法的优化方案相当多:kdtree的、基于网格计算的、基于适应性解算阈值的、局部敏感哈希。主要解决的都是如何加快求解邻域解求速度。诚然它的算法复杂度有n^3显然想要加快并不是那么容易。深入研讨了一番发现计算距离时有的不止一遍,因此写入硬盘或许是个好的方案,但是I/O读取的效率就要考虑进来了;还有一种方式是限制深入迭代次数,即做多在第几层nearestpoint()这个数组中进行聚类的拓展。这种做法的危害是使得同一个点集很可能多次才并入,或者完全没有并到一块,因此需要一个后手,将聚类中心相近的再次组合,其实在kdtree中也有类似的做法。参考基于SPark的DBSCAN的图解,KDTree建立时,按区域分割好数据后,同一类的点集亦可能先分散于个个区间。各自区间先进行小聚类后,再进行大聚类。
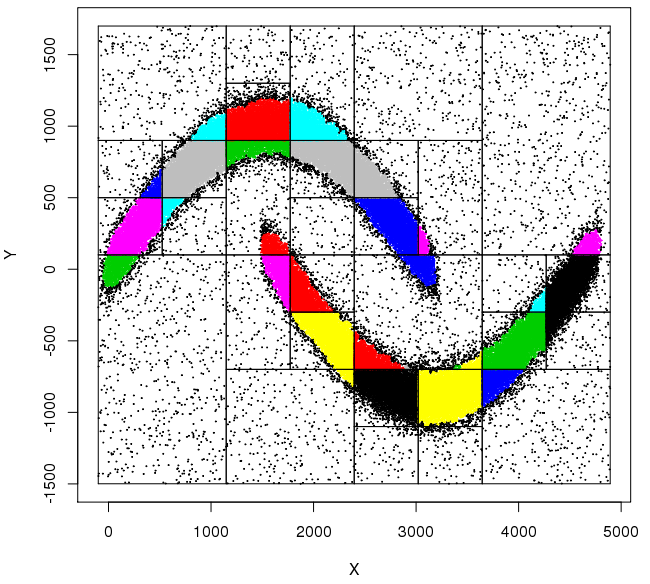
(中了SPark的毒,后面会进行测试)
demo很好的展示了算法的原理。
http://www.naftaliharris.com/blog/visualizing-dbscan-clustering/ 在线666可视化理解dbscan过程。不同的实例可以看到,对不同图形的检测相当准确;同时聚类精度亦相当高。
http://stackoverflow.com/questions/6621630/dbscan-code-in-c-sharp-or-vb-net-for-cluster-analysisstackoverflow图解dbscan
https://www.yzuzun.com/2015/07/dbscan-clustering-algorithm-and-c-implementation/ dbscan的C#实现和作者的gayhub项目
http://download.csdn.net/detail/f112122/7482303 c#简易可视化工程例子
诚然,boost把很多常用的算法都写进去了。但c++使用起来才比较顺。这是c++环境下使用dbscan的正确方式:上boost。比如下面这个
https://github.com/yusufuzun/dbscan(C# 以算法原理为基准 不是很快)
或这个https://github.com/Terranlee/DBSCAN(C++&boost&KDTree 至今没有明白第一个参数ire的含义啊。一般都2个参数就好了啊 而且结果貌似也不太对 等待修正)
boost的使用
上边两个github的例子都基于c++开发,其中都使用到了流行的c++高性能计算类库boost。
linux下的编译和安装遵循这个帖比较顺
http://ju.outofmemory.cn/entry/106397
KDTree
KDTree作为一种数据结构的拓展,其实是一种变异的二叉排序树,其最最最原始的构造就是,在二叉树左小右大的基础上,对多维数据,第一层比较第一个维度,第二层比较第二个维度,以此类推…………排到最后一维又返回第一位继续排,当然,而已设定排序的次数,到多少维就懒得排了。这个数据结构的好处是,寻找欧几里得空间(也就是任意维度的两个对象的连线长度&有的地方也使用该值当做两个对象相似度)的最邻近点(集)复杂度大大降低,不用迭代整个数就能找到最近的点。
上面说的DBSCAN、后面的ICP、图像匹配中的SIFT算子比较相似度(128维),使用KDTree可以很好的解决时间太长的问题。
来一波树形结合,
KDTree的改进方法有Best Bin Fisrt、Best First Search。它主要的临近查找是基于路径和回路的,但没有考虑节点的一些性质,BBF则根据查询路径上的节点进行排序,排序原则是按照超平面的最短距离。另外还可设置超时,优先级队列中的所有节点都经过检查或者超出时间限制时,返回当前最好结果当做近似的最近邻。这种方式在高维上效率提升很大。(尤其sift)
ICP(Iterative closest point)
点集匹配算法——两组有部分重叠区域的点集,进行拟合和对应点匹配。匹配中如果模式重复程度过高可能陷入局部最小值,因此需要对模式进行了良好的解析。
算法原理:①算法先解算归一两组点集比例尺、解算质心,将质心重合②对其中一个点集,寻找每个另一点集的最近点,解算梯度和旋转平移量③再次计算最近点,若旋转量小于阈值则停止,若大于阈值则继续②步骤。④按照对应点计算H矩阵(单映矩阵)。
第二部中的关键步骤其实就是解算每一步的迭代旋转和平移量,用到的是最小二乘法;其次,输入模式及输入顺序对匹配影像也比较大。一般的,停止迭代可以设置限差或者迭代次数。
VTK5.8的C#dll中有包含ICP最新的算法,但算法较旧,效率较低,但新版6.0+在C#上未开源,忧伤。算法中,求取最近点有三种做法,一点对点,直接找最近点,常用kd-tree实现;二点对面,求取最近的切面的一个切点,主要针对点集和曲面匹配;三点做发现与另一曲面交点,主要针对面与面配准。
mrpt类库中关于ICP的例子
http://www.mrpt.org/Iterative_Closest_Point_%28ICP%29_and_other_matching_algorithms
结合NUnit的ICP算法
http://www.codeproject.com/Articles/865830/Point-cloud-alignment-ICP-methods-compared
适应性:对自由形状的曲面适应性较好,VTK算法在LiDar数据扫描配准中应用较好。
convex hull of a set of points 点集的凸包
没啥特点。但相当基础。在外接圆计算、外接矩形计算的时候必须首先解算。demo相当完美。可直接改了用了。能把demo做的这么直白这么易用相当666了(c#)
minimal bounding rectangle for a polygon 凸包的最小外接矩形。这个算法在解求聚类、数据形态方面有很多利用。前提是前面提到的点集凸包以及点集是否按顺时针排序。同样的网站,给的demo我只能说酷炸了。(c#)包含了两种模式:最小面积和最小周长,两者相差不会很大。demo的计算原则是面积。
