openCV中有两个函数，findhomography和findfundamentalmat，长的很像。。一开始严重的弄混，以为都是求对应点投影矩阵的公式，万万没想到其实是两个完全不同的内涵。😒

opencv 中，进行图像拼接(全景拼接航摄拼接三维重建街景地图)，大致流程如下。

利用opencv提供的各类型特征点检测方法（Fast Start SIFT SURF ORB SimpleBlobPyramidAdapter DynamicAdapter 等）在图像中将感兴趣的有独特标识的点找出来,其中orb 是最近提出效率较高的检测和描述算法，金字塔算法则是更高的提高效率的算法；
利用不同的描述方式（SIFT SURF），对特征点的信息（周围的梯度、灰度相关性二进制编码等）进行描述；
利用不同原则的匹配方式（BF Flann-based等），对这些描述子（一般是多维矩阵）进行匹配（匹配中数据的输入参数的筛选Ransac方法），对匹配结果反向计算进一步的筛查，选择更健壮更有代表性的数据（knn Ransac），
最后利用findhomography找到映射矩阵，再利用affine将该坐标映射关系对其中一幅图贴到其中一幅图中。完成拼接。拼接区域涉及融合平滑。

这其中，findfundamentalmat()和findhomography()都是用来查找两组匹配坐标点的映射关系的（两组坐标几何数目相同同一数组位为同一对匹配点）试着运行了一下homography生成的矩阵拼接效果良好。而findfundamentalmat就不太6.找了一些相关资料，其实这是两个相似但不相同的函数。so开始之前科普几个概念：

核点（极点）：摄影中心连线（基线）ss’延长线，与左右影像的交点，分为左右核点（极点）。（注：下图两影像接近平行，则ss’连线与影像无交点，而在下下图中，el er分别为左右核点【极点】）亦可理解为左右摄影中心分别在对方像片的像点

核面（极面） ：过摄影基线与物方任意一点组成的平面。（所以缩，物方点不同，核面一般也不同任意一个下图的PO1O2都是核面）

核线（极线）：立体像对中，同名光线与摄影基线所组成核面与左右像片的交线。 （不同同名点极线不同，因而有很多很多条）

极线约束 ：同一个点在两幅图像上的映射，已知左图映射点p1，那么右图映射点p2一定在p1的外极线上，这样可以减少匹配点数量。

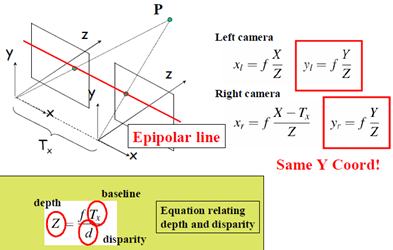
上图中，红线即为极线，物方点P（X,Y,Z）分别在左右两图留下了同名点（xl，yl）、（xr,yr）。Tx即为基线长。但上图为两个平面接近平行且z方向接近0，但一般情况下，两像平面以任意角度成像同时内参数并不相同，因此上图中的极线呈现出共线的情况，更多的情况是下面这个图，两图像成任意角度。

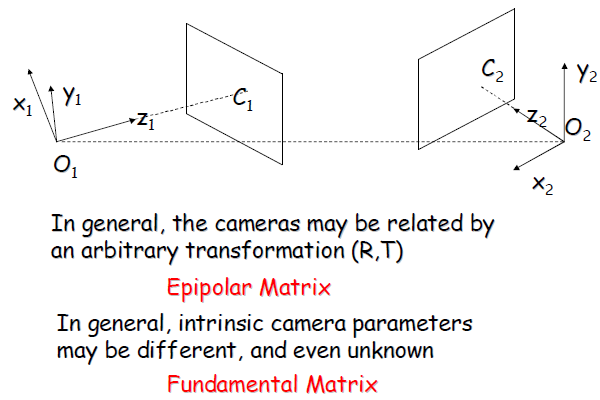
下图中，O1O2连线与左右像平面交点el和er即为左右极点(极点亦可理解为左右摄影中心在另一像平面的像)，而极线则为plel和prer。可以看到，这两条线显然就不平行了。

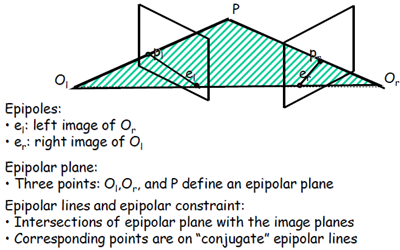
基线：相邻两摄站点（摄影中心一般标为s）之间的连线。

主核面 ：左右像主点分别与基线构成的平面，分别称为左主核面和右主核面。

灭点vanishing point：平行线在二维图像中汇聚的地方，空间中每一组平行线都有自己的灭点。

灭线vanishing line（消隐线） ：不同的灭线连线，即灭线。如果两组不同的平行线，都平行于大地，则他们的连线就是地平线（horizon line）

第一个矩阵Essential本质矩阵

由于拍摄物体时，摄影中心并不能被反映在图像中。如果让第二个观察者同时拍摄下某摄影中心和它所拍的照片呢?

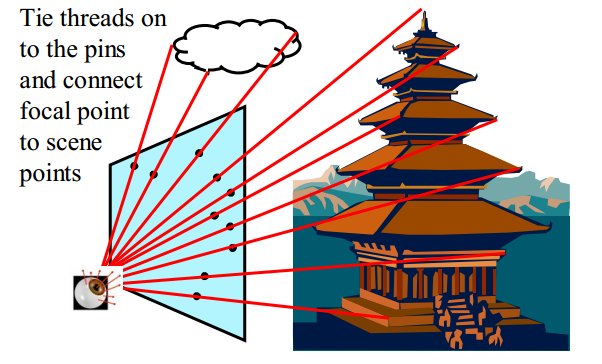
反映在第二个观察者的照片，摄影中心和物体分别投影在像片上，任意第一个摄影中心和它所拍摄物体的连线都可视为第二个摄影中心的极线。直观的理解，即为下图的erpr。

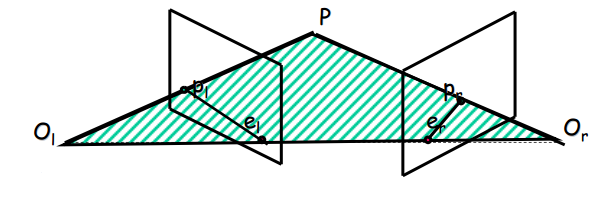
极线约束的理论就是左侧的物体成像在右侧的同名点一定在erpr上。反映左右极线关系的就是表达向量和右向量之间的约束关系的——本质矩阵即Eseential Matrix。但大多数情况下，别的摄影中心并不一定会被成像，即极点不在相片中。如下图

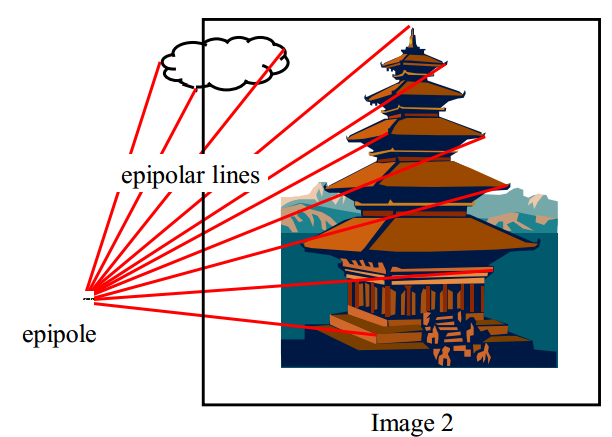
具体的矩阵运算参考 计算机视觉基础4——对极几何(Epipolar Geometry) ，原理为三线同面（下图蓝色区域三边）

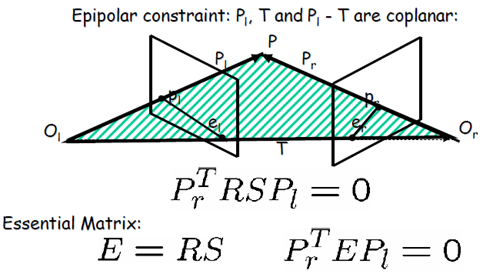
其中，E是本质矩阵（Essential Matrix），R是像平面旋转矩阵，T是摄影中心平移矩阵，Pl和Pr分别为左右摄影中心指向同名点P的向量。S由矩阵T决定，具体形式为

本质矩阵 采用的是相机的外部参数，也就是说采用相机坐标(The essential matrix uses CAMERA coordinates)，不涉及相机内参数，如果要分析数字图像，则要考虑坐标(u,v)，此时需要用到内部参数(To use image coordinates we must consider the INTRINSIC camera parameters)

谨记1：Essential Matrix是连结两个摄影中心指向同名点的向量的矩阵，秩为2。

左向量·E·右向量=0！！！

E由两部分组成！E=R·S E仅由外方位元素决定！一张图记住E!!!

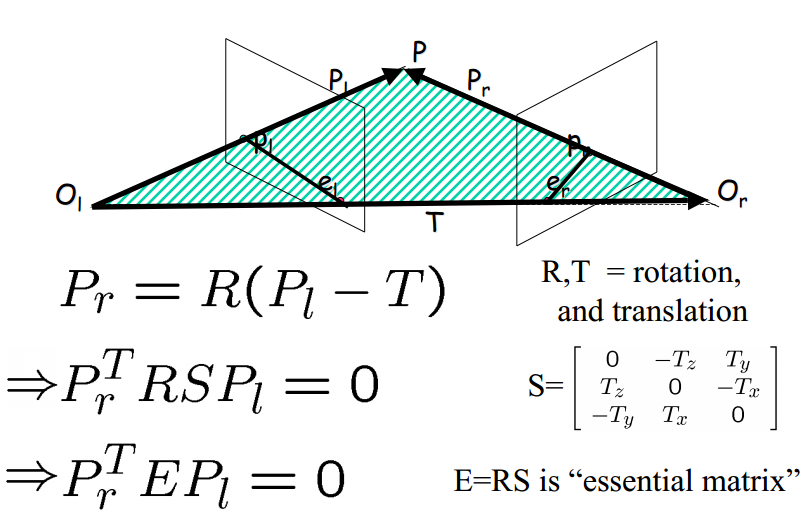
上式Pr Pl均基于物方三维坐标。同理由向量引申而出的，则是同名点的像素坐标，原理是共线方程。

二维同名点

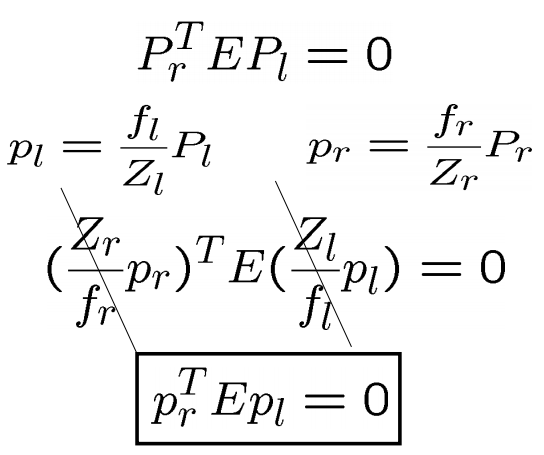
上图中推导出对极几何中相当重要的公式，E矩阵作为连接同名点像素坐标而出现，这就意味着，已知求取E的外方位参数，就能求取出左右同名点的对应关系。然而，其中隐含的条件是在共线方程的化简中，默认忽略了镜头畸变。然而这已足够重要，在镜头畸变在拼接中影响不大时，该公式在仅仅知道外方位元素的情况就能解算corresponding point

极线方程

同理，由于极点、同名点都位于极线上，因此亦可通过E求得极线的方程（采用相机坐标系）。

设极线方程为 au + bv + c = 0

使用齐次坐标，矩阵表示为：

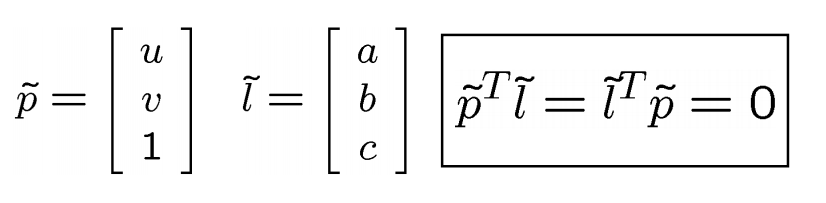
其中，$\widetilde{p}$是像片任意同名点相机坐标，$\widetilde{l}$是方程系数。又依据同名点公式，$$Ep_{l} =\widetilde{l_{r}}$$，所以！对应外极线的方程系数可以直接由E矩阵和本侧同名点求出。其中，$\widetilde{l_{l}}$是左极点对应外极线方程。

当已知左侧点，其右侧对应点在直线

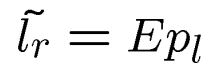
当已知右侧点，其左侧对应点在极线

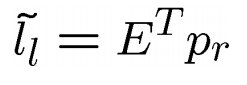
极点

别忘了。极点也是在极线上，所以有

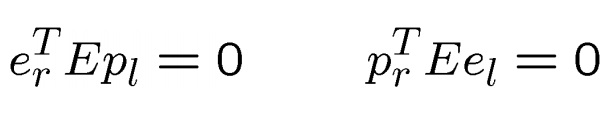
且，极点属于所有极线，因而

上式可用来定位极点的坐标

# 第2个矩阵 Fundamental基础矩阵

另一个需要提到的概念是基础矩阵。

Essential矩阵使用CameraCoords相机坐标系。尽管其中可计算像素坐标，但仍然以摄影中心为原点，像平面所有点z值都是f。当考虑相机内参数时，这就是FundamentalMatrix基础矩阵

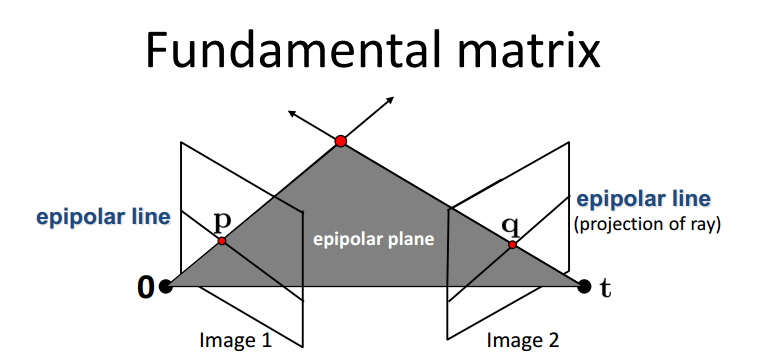
该图显示了fundamentalmatrix（基础矩阵）的基本内涵。p q分别为同名点。计算基础矩阵需要考虑到内参数的仿射变换。M为内参数的矩阵，包含6个参数的33矩阵。

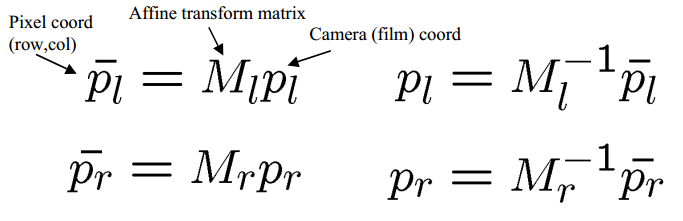
将上式中的Camera坐标提到一边，带入基本矩阵解求对极同名点的方程，即可得到F的表达式.

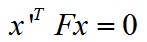
上式即为基础矩阵方程。其中，F是基础矩阵，x’x分别为同名点。而左右两个平面的两条极线为，显而易见，F由E和两个内参数矩阵决定。

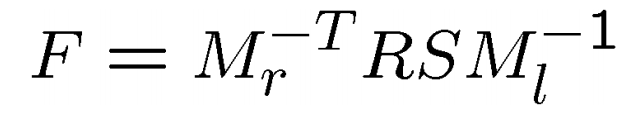
类似的，F与E一样都能指同名点坐标在对应极线的关系。下图分别是已知左右点其对应极线的关系。

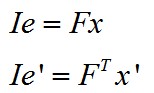
一个简单的例子，如果从某种方式计算出基础矩阵，则在对应图中即可表示出像素点对应的极线。

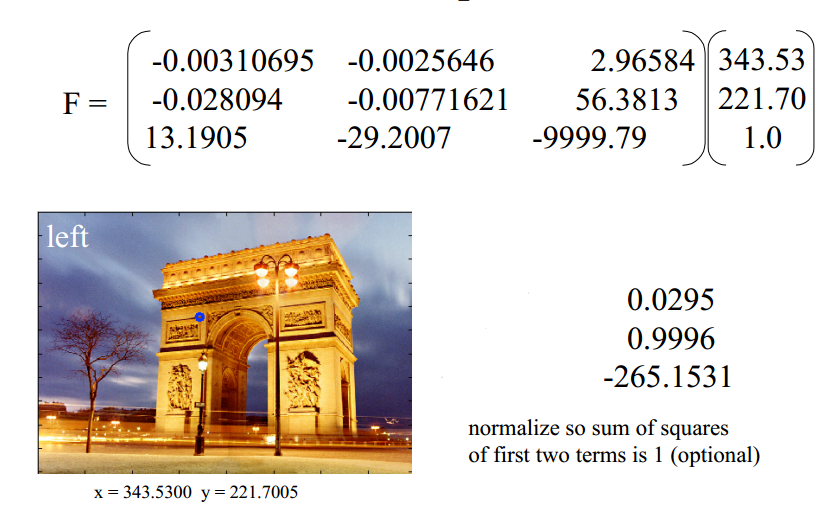
计算出矩阵即为l的三个参数。一般的，调整比例将前两项的平方和定为1.

findfundamentalmat()本意为基础矩阵，是假设两幅图像在同一三维场景中的不同视角。例如立体摄像机，从不同的角度拍摄同一个目标，它解算的是，两幅图像其中一个同名点，与其在外极线同名点的转换关系。它的映射基于三维场景，因此使用这个函数的时候，在不同的视角之间，应该有一个明显的基线。默认使用7点算法拟合数据。基础矩阵把左边图像的一个点的图像坐标与它右边图像中的对应点的图像联系起来，他是一个3x3的退化矩阵，描述了两个立体图像对的外极限几何关系，其计算依赖于在两个图像中相对应的一组点。

与Homography矩阵（下文提到）不同，它在每组对应点有两组约束：x、y同时作为x’y’的自变量，估算一组对应点只有一行的约束，因为极线约束是标量等式。因此至少需要8个点。所以一般使用8点算法计算F矩阵(8点算法)。

$$\begin{bmatrix} x^{‘}_i & y^{‘}_i & 1 \end{bmatrix} \begin{bmatrix} f_{11} & f_{12} & f_{13} \\\ f_{21} & f_{22} & f_{23} \\\ f_{31} & f_{32} & f_{33} \end{bmatrix} \begin{bmatrix} x_i \\\ y_i \\\ 1 \end{bmatrix}=0$$

可推到出方程：

$$ x_i x^{‘}_i f_{11} + x_i y^{‘}_i f_{21} + x_i f_{31} + y_i x^{‘}_i f_{12} + y_i y^{‘}_i f_{22} + y_i f_{32} + {x_i}^{‘} f_{13} + y^{‘}_i f_{23} + f_{33} =0$$

最终目标是找到ATA的一个特征向量使得它的特征值最小。常用的解法是构造m*9的矩阵A（m是点对数），求解A的奇异值分解，即A=UDVT，

U是m*m正交矩阵，其列为AAT特征向量

V是m*n正交阵，其列为ATA的特征向量

D是m*n对角阵，对角元素为奇异值，平方值为AAT和ATA的特征值。

然而F是由7个自由度构成的3*3矩阵，其秩为2，因此，讲道理，9个表达式由7个参数构成，因此只用7对对应点理应也能解算出F矩阵（7点算法）。使用此方法计算F矩阵时，需要加上秩为2的限制，以保证计算结果唯一。该方法亦叫做奇异约束。该约束限制假设以F’替代F矩阵，计算时以F范式作为标准。

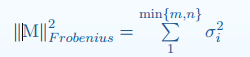
其中，$\sigma$是M矩阵的奇异值（A*·A的n个特征值的非负平方根叫作A的奇异值），M=F-F’,可以通过SVD分解解出该奇异值。

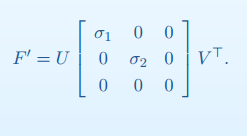
F由于秩为2的限制可以以以下形式表示：

F=αF1+(1-α)F2.其中，F1和F2分别Fx=0的两个解。

由于秩=2，因此det(F=αF1+(1-α)F2)=0,通过该式即可求出α的值。

更多内容可以看计算机视觉Trifocal tensor三角点张量的部分。

Caution!

对图像进行匹配的一个重要步骤就是把两幅图像的极线平行于基线，使得极点处在正无穷，这样的拼接结果效果才能更好。这一重要步骤即为重投影。如下图将黑线投影为蓝线。

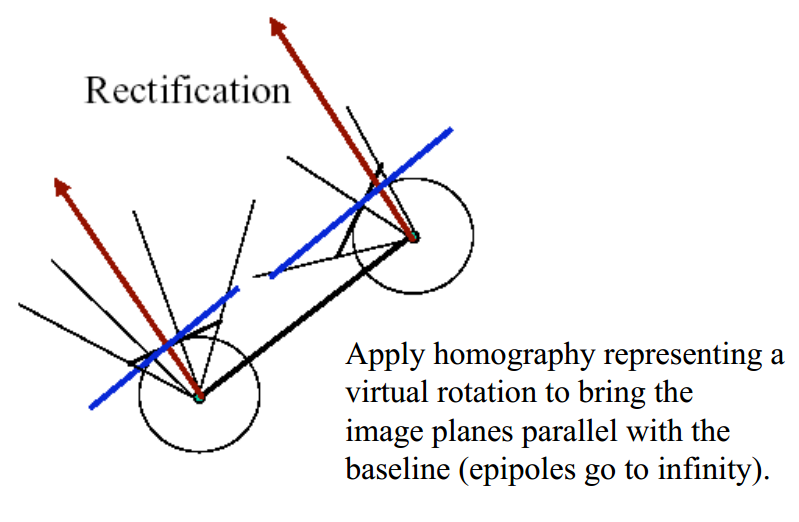
对图像进行矫正。需要一个单映矩阵，作两步旋转。其第一步是将极点旋转到无穷远，第二部是将极线平行。其中，左右图像均需要应用该单映聚阵R将极点无穷远化；而右图像需要应用旋转矩阵（E=RS中的R）。最后比例一致化。

上文中需要构造的矫正矩阵形式为：

T是单位矩阵，代表左图的极点，可由E计算。其余的参数：

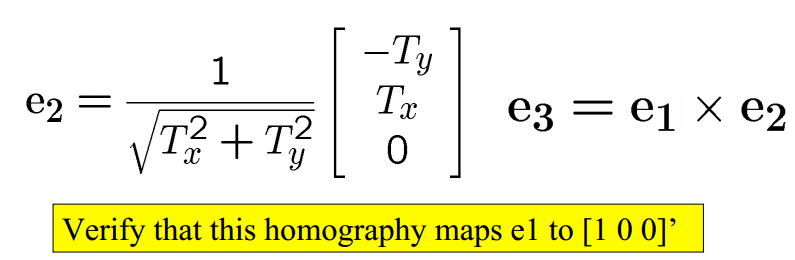
整理一下步骤即为：

下图即为矫正的例子（两幅图的变化很小，但是从边缘还是可以看到细微的变化），最后把图像的极点都化为无穷远，两幅图基于基线平行。

第二个矩阵 Homography（单映）矩阵

findhomography的前提是2D的转换，本意为单映（包含平移、仿射、尺度三种变换），试图找到一个3*3的投影矩阵，能够把1图中所有的点，通过某种形变，匹配到2图中去。当基线很小的时候(视差变化小，扭曲形变也少)，这个方法能够计算出精度极高的解。
当然可以首先参考opencv的文档这里首先介绍二维映射的单映（homography）矩阵

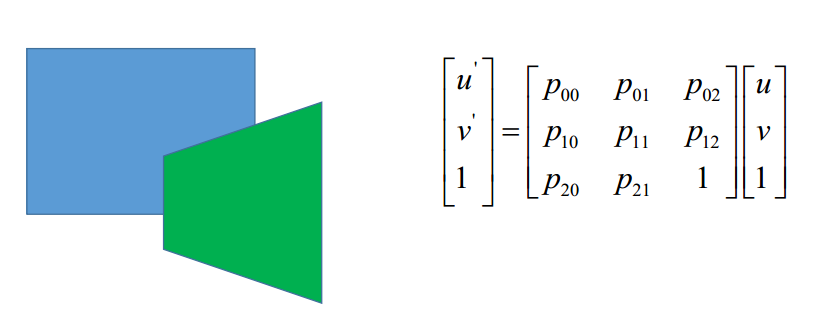
该式反应了像点齐次坐标的单映变换的方程。（u v）(u’ v’)分别是左右图像的同名像点坐标。通过一个8个自由度的矩阵P来解算两者之间的关系。p02 p12与平移相关，p00,p01,p10,p11与旋转尺度和仿射（平行变换）变换有关，p20,p21与拉伸扭曲有关。

一般的，单映矩阵的计算由以下几个参数构成

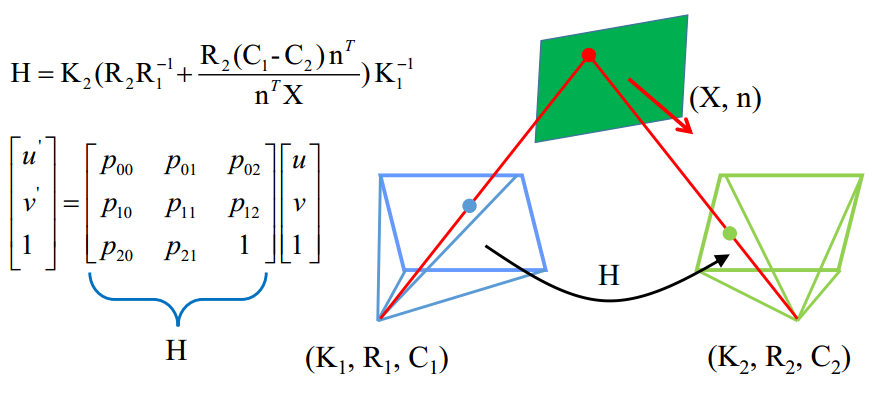
其中，K是相机的内矩阵，由焦距决定；R是主光轴朝向，一般由3个方向余弦决定；C是摄影中心的物方位置。当在原地旋转时，C1-C2为0，因此方程可简化为

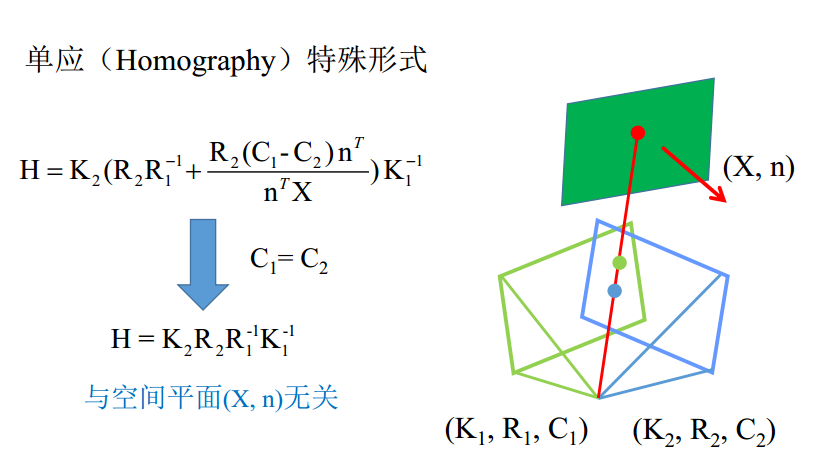
由相机纯粹旋转而形成的单映，自由度3-5（根据是否已知焦距决定）。

Caution！应该注意到的是，上式中的H3*3矩阵的最后一个元素为1。这里使用到的是计算H矩阵最常用的一种方法，4点算法，即使用4个点即可解算一组H中的8个未知数。在ransac验证外点的过程中，也采用随机4点为一组构建8个方程解算H。

尽管homography是处理二维点集之间的关系，但倘若三维物体中某些点都处于一个平面，即可设该面的z方向值为0，以三维物方xy值作为像素值与所成像片进行homography的变换。

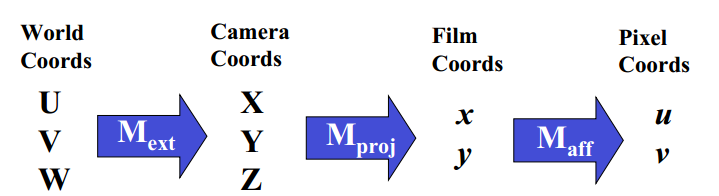
上图是几种坐标系之间的关系，Mext是外参数矩阵，包含旋转和平移；Mproj是投影矩阵，主要由焦距决定，原理是共线方程；Maff是内参数仿射变换矩阵，由内参数决定。普通的homography是两幅图像像素坐标间或相片坐标间的变换，但上文提到，当三维物体某些点处于一个平面，亦可在World坐标和Film坐标之间进行homography矩阵变换。

上图可以看到，将三维坐标点z值设为0，[p,q,0,1]即为三维齐次坐标。

$$ \begin{bmatrix} x\\\ y \\\ 1
\end{bmatrix} \sim \begin{bmatrix} f & 0 & 0 & 0 \\\ 0 & f & 0 & 0 \\\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_x \\\ r_{21} & r_{22} & r_{23} & t_y \\\ r_{31} & r_{32}& r_33 & t_z \\\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} p \\\ q \\\ 0\\\ 1 \end{bmatrix} \sim \begin{bmatrix} fr_{11} & fr_{12} & ft_x \\\ fr_{21} & fr_{22} & ft_y \\\ r_{31} & r_{32} & t_z \end{bmatrix} \begin{bmatrix} p \\\ q\\\ 1 \end{bmatrix}
$$$$\sim \begin{bmatrix} h_{11} & h_{12}&h_{13} \\\ h_{21} & h_{22} & h_{23} \\\ h_{31} & h_{32} & h_{33} \end{bmatrix} \begin{bmatrix} p \\\ q \\\ 1 \end{bmatrix}$$
最终推到出，3D转2D的投影变换成为2D转2D的变换，该变化可逆！其特例是，当采用的物方坐标系z轴与主光轴平行，即正射影像，则上式R矩阵为

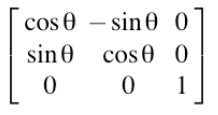
则上式变形为：

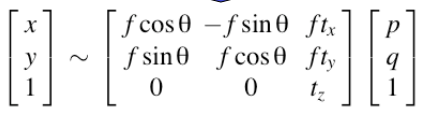
该式与相似变换的形式一样，只有4个自由度（tz可化为1），因而正射影像不会产生拉伸形变。（前提是拍摄物体几乎没有深度，几乎处在一个平面）。下图是依照三维中某平面进行拼接，会造成除平面部分其余图像的虚影。

上文中一直讨论的是从物方坐标系到像片坐标系的转换，倘若再加上内方位参数的内矩阵，则可直接导出从物方坐标到像素坐标的公式，如下图示意。内方位参数为仿射变换（Affine 6自由度保持平行结构的变换）

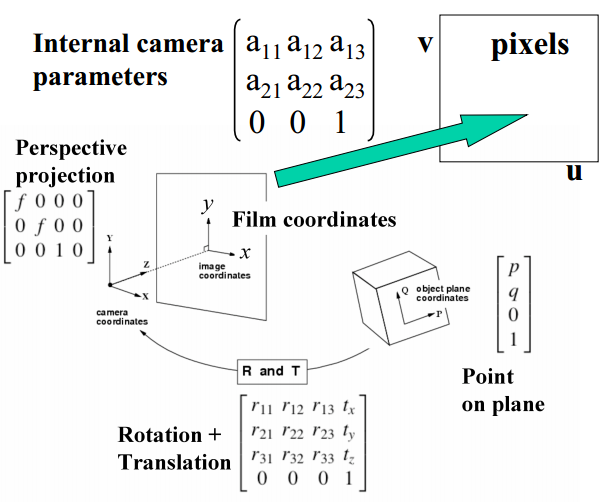
将world->film->pixel结合起来，对于同一个物体，在某位置某台相机拍摄的照片就可以认为是一个单映H。当然，不同的位置拍摄的像片，各自对应物体的单映是不同的。但由于单映是可逆的，拍摄同一物体的两幅图像，也可以用使用$$H=H_{1}H_{2}^{-1}$$

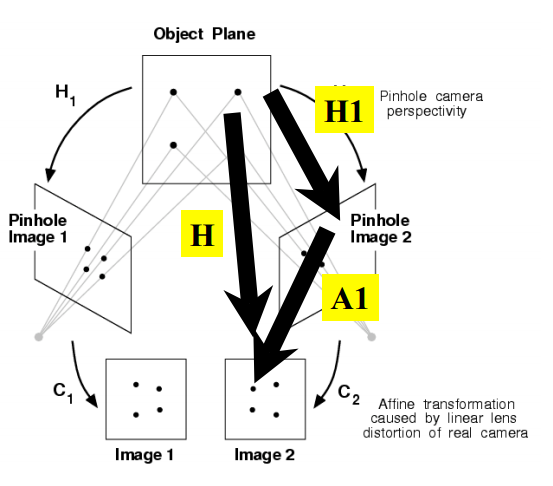
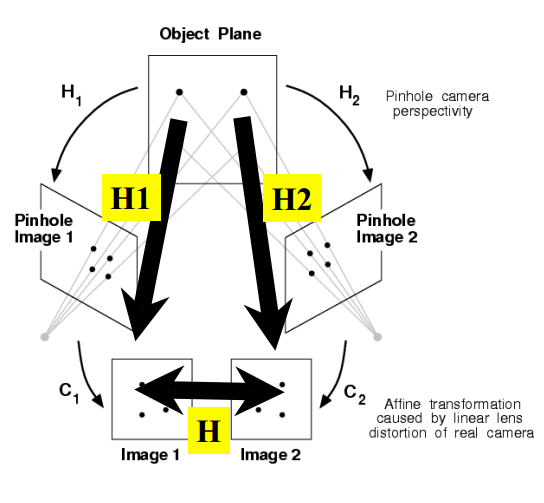
Homography（单映）矩阵的求取

参考这里只要大于4个匹配点，都认为是冗余测量，必须融合数据。文章里提到了三种解求二维面到面的单应矩阵的球法。

非线性的解决办法，使用伪逆进行分解。当所解求值为0时会有bug。
线性最小二乘解法，通常使用SVD分解，V矩阵就对应了最小奇异值。这个SVD的文章相当好的解释了SVD分解的意义。八个未知数对应八个特征向量，也对应八个线性方程的解。SVD能直接解求出这八个向量，即V中的特征向量。
非线性几何解法，使对应点和映射点差值欧几里得距离（或平方和）最小。

Homograhy的计算：计算该矩阵当然不会上式f θ等值直接解算。由于是二维图像之间的关系，一般都已知二维对应点集，直接采用最小二乘的方式使用LM进行计算。在一般情况下的H矩阵可表示为

$$ \begin{bmatrix} x^{‘} \\\ y^{‘} \\\ 1 \end{bmatrix} \sim \begin{bmatrix} h_{11} & h_{12} & h_{13} \\\ h_{21} & h_{22} & h_{23} \\\ h_{31} & h_{32} & h_{33} \end{bmatrix} \begin{bmatrix} x \\\ y \\\ 1 \end{bmatrix}$$

其中，$h_{31} h_{32} h_{33}$是为了配置相似比例，化简为

$$x^{‘}=\frac{h_{11} x + h_{12} y + h_{13} }{ h_{31} x + h_{32} y + h_{33} }$$

$$y^{‘}=\frac{h_{21} \cdot x + h_{22} y + h_{23} }{ h_{31} x + h_{32} y + h_{33} }$$

但可以看到，h所有元素同乘k 等式依旧成立。因而强制设为8自由度有两种方式，

①$$ h_{33} = 1 $$

②$$ h_{11}^{2} + h_{12}^{2} = 1 $$
采用第一种方式较为常见。
当采用最小二乘解求H矩阵时，一般先用Ransac筛选最大集，然后利用下方程。

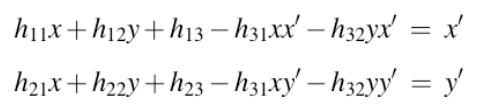
以x y x’y’为A b矩阵参数，迭代解求H。由于是线性方程，因而可以直接使用$$h=(A^{T}A)^{-1}(A^{T}b)$$求取每次的残差。

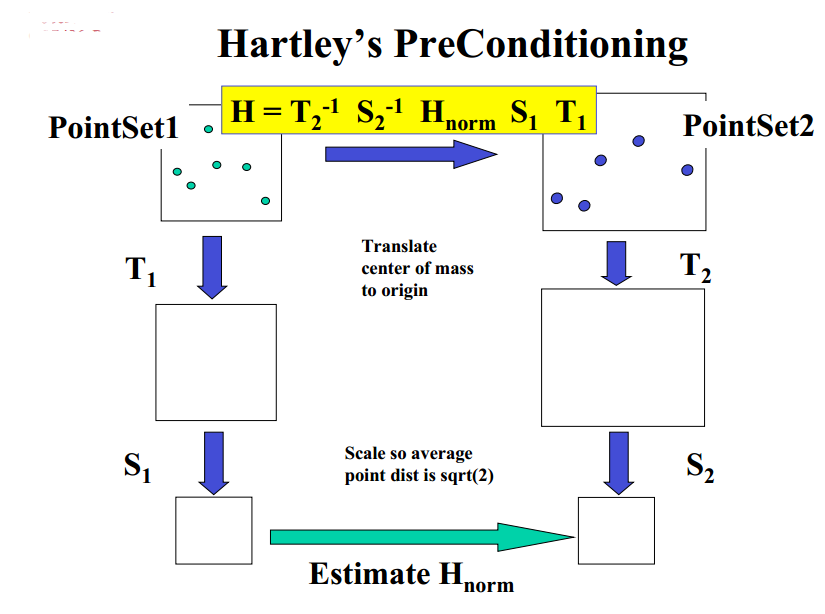
<font color=”#ff0000”>Caution！应该注意到的是，该方法对噪声极其敏感，即使没有外点（outliers）,因而，在计算前对数据里筛选就非常重要。为更好的得到结果，Ransac时可以将该组数据质心重置到原点；然后缩放比例使得各点到原点的平均距离是根号二。如下图，H的表达式。T、S分别为平移和缩放的矩阵。

如何判断这两幅图像确实匹配呢？记该区域的特征点总数为nf，而符合H的特征点（内点）数量为nj，如果两者比例足够大，说明两幅图像确实匹配。但一般拼接时都确认两幅图像有重叠面积才计算H。变换模型H计算时的误差可表述为Huber模型：

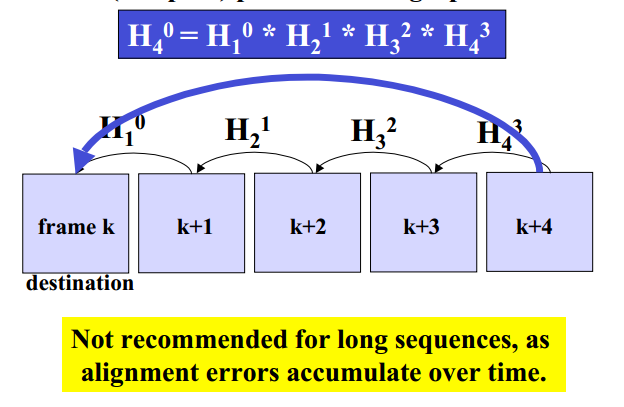
同时，由于矩阵具有可逆性，因此图像12之间的H1和图像23之间的H2可以直接推导出图像13之间的H3。但大量的单映队列并不推荐，这样会造成误差成倍扩大。

谨记二 ：homography处理的是纯粹的二维与二维之间的变换。即便特例是3D也是视为在2D的单映和相似变换。在旋转相机和正射拼接可以得到良好的二维拼接效果，在具有深度的三维物体，拼接会造成虚影！

这两个函数都是基于特征点的变换模型求解，既然特征点已找出且筛查得到更正确的点，因此对图像外观的变化具有鲁棒性（尺度、光照、旋转等）。选择哪种函数基于图像间的关系，即立体场的观测使用fundamentalmatrix（视角矫正三维全景街景视角）,而相对平面化的则使用findhomography（全景拼接航摄图像拼接）

解求这个变换模型一般基于线性最小二乘的方式，与平差原理类似，利用冗余的数据（大量同名点）来解算参数。一般的，先通过Ransac筛查数据比较靠谱。